1. 引言
自旋波是磁有序体系中的集体激发行为,其量子化载体被称为磁子。磁子可以作为信息的载体,而且磁子的输运不涉及电荷的运动,因此基于磁子学的自旋波器件在近年来吸引了相当大的基础研究和应用领域的兴趣。
2019年,贾成龙等人 [1] 首次在均匀磁化的圆柱形铁磁体中激发携带轨道角动量的自旋波。这种自旋波的波阵面为绕样品中轴线旋转的螺旋面 [2] ,其与方位角φ的依赖关系可以表示为
,其中是 涡旋自旋波的拓扑荷数。l代表相互交织的等相位面的数目 [3] [4] [5] 。2020年,闫鹏等人[5]提出涡旋自旋波的轨道角动量可以驱动磁斯格明子产生旋进运动。文献 [1] 和 [5] 所报道的工作所采用的驱动磁场为拉盖尔-高斯型光场。该型光场本身携带轨道角动量,因此可以认为它所激发的自旋波所携带的拓扑荷来自于激励磁场的拓扑结构。但是,这样携带拓扑荷的光场需要复杂的技术设备。并且计算显示,需要使用超高功率的拉盖尔–高斯型激光才能激发出涡旋自旋波。2022年,黄培源等人 [6] 设计了一个厚纳米圆盘,其基态为磁涡旋态。在底部的局域的旋转磁场激励下,产生的自旋波在角向和轴向传播,形成了激发携带轨道角动量的自旋波的新颖方式。但是,这种方法难以产生高拓扑荷数的涡旋自旋波。此外,利用螺旋相位波片 [7] 、两个相互耦合的铁磁圆盘 [8] 及磁涡旋态和条形纳米条带的耦合结构 [9] 等,研究者发现了产生涡旋自旋波的不同结构和物理机制。总结来说,这些工作中所使用的样品都具有圆周对称性,涡旋自旋波的拓扑荷可以认为是由激励磁场、螺旋相位片或者样品的磁矩拓扑结构所“压印”产生的。在这些工作中,自旋波的角动量与波矢量的方向平行,即它们均沿着样品的对称轴方向。因此其轨道角动量被称为是纵向的。
携带横向轨道角动量的波最早在光波中发现,2022年,万辰皓等人在实验上利用光脉冲整形器产生了携带横向轨道角动量的时空涡旋光场,并重建了时空面上的涡旋光场相位分布图,这是一个中心为相位奇点的涡旋相位分布 [10] 。在这里,我们展示一个准二维的铁磁纳米条带,在摆动磁场的激发下产生携带横向轨道角动量的自旋波的机制。不同于其它携带角动量的波,我们所报道的自旋波在一个准二维样品中传播,它所携带的轨道角动量不但与波传播方向垂直,而且其角动量的方向在一个波长中发生两次翻转。
2. 样品模型
我们的坡莫合金样品长2200 nm,宽100 nm,厚5 nm,其初始态磁矩如图1所示。我们采用基于有限差分法的OOMMF软件 (Object Oriented Micromagnetic Framework) [11] 进行微磁模拟计算。样品的参数设置为:磁晶各项异性常数K= 0 J⁄m3;饱和磁化强度MS= 8.0 × 105A/m;交换相互作用系数A = 1.3 × 10−11J⁄m,阻尼系数α= 0.01。样品被划分为2 × 2 × 5 nm3的网格。为了消除自旋波在样品左右端所产生的反射波,我们在纳米带两端分别设置了10个宽度均为10 nm的吸收端,从样品左右两端开始,阻尼系数依次为1.0、0.82、0.65、0.5、0.37、0.26、0.17、0.1、0.05和0.02。

Figure 1. The initial magnetization distribution in a ferromagnetic nanostrip with a length of 2200 nm and a width of 100 nm, as shown by the arrow
图1. 长2200 nm、宽100 nm、厚5 nm的铁磁性纳米条带示意图。黑色箭头表示样品沿+x方向均匀磁化的初始态,红色虚线框表示激励磁场的施加区域,左右两端的蓝色虚线框表示自旋波吸收区域
3. 携带横向轨道角动量的自旋波的本征频谱及其模态
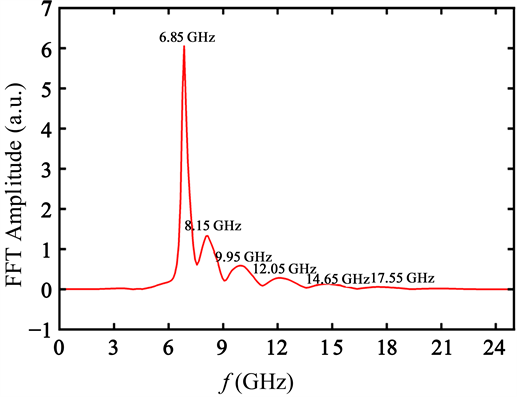
Figure 2. FFT amplitude spectrum of spin waves in ferromagnetic nanoribbons after applying a swinging field on the sample
图2. 对样品施加一个周期的摆动磁场后,对磁矩y分量的平均值随时间变化进行快速傅里叶变换后,得到的自旋波频谱图
为了了解样品内激发的自旋波的本征模态,我们在x= 1076 nm~1124 nm的区域施加一个周期的摆动磁场。该磁场方向位于y-z平面内,且其初始方向沿−z轴,然后在−z轴和+z轴之间来回摆动一个周期。这个摆动场的数学表达式为:
(1)
摆动磁场的振幅0= 100 mT,频率为
。在接下来10 ns内,微磁模拟运算记录下每个格点的磁矩随时间的变化,然后我们对x= 1076 nm~1124 nm的范围内的磁矩振动y分量的平均值〈my〉做快速傅里叶变换,得到如图2所示的自旋波频谱图。其中频率为6.85、8.15和9.95 GHz的峰对应于平面自旋波模态。但是,频率为12.05、14.65和17.55 GHz的模态对应携带横向轨道角动量的自旋波。
为了进一步验证携带横向轨道角动量的自旋波的存在,我们对特定频率下的磁矩振动模态进行反傅里叶变换(IFFT)。我们分别取了自旋波频谱上本征频率为12.05、14.65和17.55 GHz的点,对沿x轴正方向传播的自旋波的磁矩振动模态进行反傅里叶变换。为了更加确定自旋波携带了横向轨道角动量,画出相同区域磁矩振动的相位图。得到的自旋波模态图和相位图如图3所示。
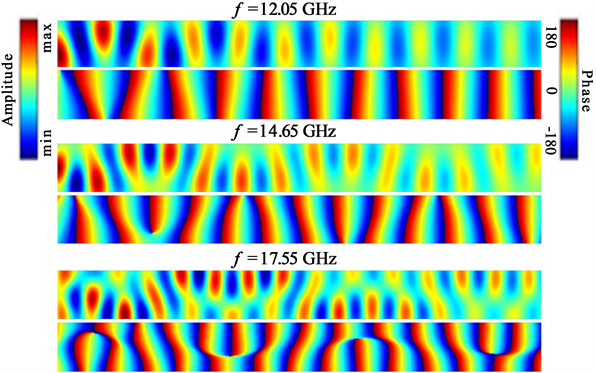
Figure 3. Amplitude and phase diagrams of spin waves with resonant frequencies of 12.05, 14.65, and 17.55 GHz, respectively
图3. 本征频率为12.05 GHz、14.65 GHz和17.55 GHz的自旋波模态的振幅分布图和相位分布图
从磁矩的振幅分布图可以看出,频率为12.05、14.65和17.55 GHz的自旋波在向右传播的过程中波峰和波谷会交替出现,试想一下,如果把每个波峰上振幅最大的点连接起来,或者把每个波谷上振幅最小的点连接起来,可以想象到这是一条曲线而不是一条直线,换句话说,就是这三种本征频率对应的自旋波其波矢k经过的路径不是一条直线,而是一条曲线。这与波矢k走直线的平面自旋波完全不同。另外从相位分布图上可以看出,这三个本征频率的自旋波,其等相位面随着距离x的不同而发生了不同程度的偏转,即等相位面与+y轴的夹角在不同的x位置处并不相同。如果单独看某一条等相位面,就会发现,这些等相位面并不是一条直线,而呈现为曲线。这清楚表明,本征频率为12.05、14.65、和17.55 GHz的自旋波携带了轨道角动量。又由于等相位面是在x-y平面内旋转,因此自旋波携带的轨道角动量是沿着z方向。根据等相位面旋转方向的不同,轨道角动量既可沿着+z方向,也可沿着−z方向。无论轨道角动量是沿着+z方向还是沿着−z方向,它都与+x方向即自旋波的传播方向垂直,也就是和波矢k垂直,因此可以确定这三个自旋波模态携带的轨道角动量为横向。
仔细观察还可以发现,对于本征频率f= 12.05 GHz的自旋波来说,最靠近波源的等相位面弯曲最明显,随着自旋波在+x方向的传播,其等相位面渐渐变为沿y方向的平直形状,几乎和平面自旋波的等相位面相同,这表明自旋波所携带的横向轨道角动量在自旋波的传播过程中会逐渐丢失。相应地,携带横向轨道角动量的自旋波就会变为平面自旋波。对于本征频率f= 14.65 GHz的自旋波来说,它的等相位面弯曲程度较大且在自旋波的传播过程中其携带的横向轨道角动量丢失不明显,可以看到最靠近纳米带右端的那个等相位面依然有明显的弯曲。对于本征频率f= 17.55 GHz的自旋波来说,可以看到其等相位面有些发生了断裂,有些则出现了两个等相位面粘连在一起的情况,这表明其等相位面结构更为复杂。下面,我们选取频率f= 14.65 GHz的自旋波进行详细的讨论。
我们对样品施加f= 14.65 GHz、持续时间为3 ns的连续摆动场,其数学表达式为:
(2)
摆动场的分量随时间变化如图4所示。依然对1124 nm ≤x≤ 2100 nm范围内的磁矩振动模态进行反傅里叶变换,得到的自旋波振幅图和相位图如图5所示。

Figure 4. Variation of theyand z components of the continuous swinging field. The field frequency is 14.65 GHz, and the time duration is 3 ns.
图4. 本征频率为14.65 GHz摆动场的y和z分量随时间的变化

Figure 5. Amplitude and phase diagrams of spin waves in the ferromagnetic nanostripe after applying a swinging field with frequency of 14.65 GHz
图5. 施加本征频率为14.65 GHz的摆动场后,铁磁性纳米条带内自旋波的振幅图和模态图
与施加一个周期的脉冲摆动磁场所激发的自旋波模态图相比,在施加连续摆动的摆动场后,除了靠近场源的第一个等相位面弯曲程度仍较大外,其余各个等相位面的弯曲程度都有不同程度的减小,即如果把每个等相位面上相位相同的那些点连接起来,这些点的分布大致形成一条直线。相同的是,本征频率f= 14.65 GHz的自旋波的波矢量走的路径依然是一条“S”型曲线,这说明该本征频率下的自旋波所携带的横向轨道角动量的方向不仅与波矢k垂直,而且还在−z方向和+z方向之间来回交替变换,这一现象在相位图上表现为等相位面沿着+y方向以不同的角度且按照一定的规律左右摆动,此外,该本征频率下的自旋波所携带的横向轨道角动量丢失依然不明显,自旋波传播到样品最右端时依然携带较为明显的横向轨道角动量。另外可以看出第一个等相位面与第二个等相位面发生了粘连,相比后面的等相位面来说更为复杂,因此在后续画等相位线时出现了误差,但对整个研究结果来说影响不大。
4. 携带横向轨道角动量的自旋波的等相位线及波速大小
为了更精确的描述,我们把每个等相位面上相位等于0的那些点连起来,形成一条条等相位线。由于格点尺寸为有限大小,在计算每个格点处的相位时会产生相应的误差。经过多次尝试,在画等相位线时我们选取的误差范围是10˚。我们选取的观察时刻分别是t= 2658、2674、2690、2706、2722和2726 ps。时间间隔正好是摆动场的一个周期,画出的等相位线如图6所示。
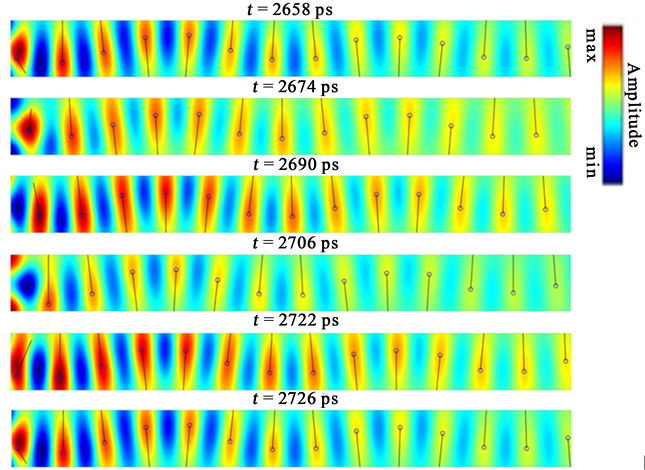
Figure 6. Isophase Lines at Different Times within a Swing Field Period
图6. 一个摆动场周期内不同时刻的等相位线图
其中黑色的直线是等相位线,等相位线的两端分别是该条等相位线上磁矩振幅最大的点和振幅最小的点,其中黑色圆圈是等相位线上磁矩振幅最大的点,所有黑色圆圈连接起来所形成的就是波矢k的轨迹,方向垂直各个等相位线且有沿+x方向的分量。从图中可以看出,等相位线上振幅最大的点大致位于自旋波波阵面的中心位置,振幅最小的点大致位于自旋波波阵面的边缘位置,由于自旋波的波前并不完整,因此等相位线上振幅最小的点有时候在样品上边缘,有时候在样品下边缘。下面我们对画有等相位线的振幅图进行详细分析。t= 2658 ps时,振幅图上有14条等相位线,随着时间的推移,所有的等相位线逐渐向样品右端移动,最后一条等相位线逐渐消失,样品中等相位线的总数量变为13条,随后,样品左端逐渐出现一条等相位线,样品中等相位线的总数量又恢复到14条,随着时间的推移,所有的等相位线继续向样品右端移动,在经过68 ps后,从摆动场开始向右数,新出现的等相位线移动到了原来第一条等相位线的所在的位置,而原来第一条等相位线移动到了原来第二条等相位线所在的位置,后面的等相位线以此类推,最终所有的等相位线基本复原,即与t= 2658 ps时样品内等相位线的排布基本相同。这说明,等相位线运动的周期大概是68 ps,时间间隔正好是摆动场作用一个周期的时间。
为了更方便的看到等相位线上不同格点振动的幅值大小,我们利用画出了三维立体图,如图7所示。
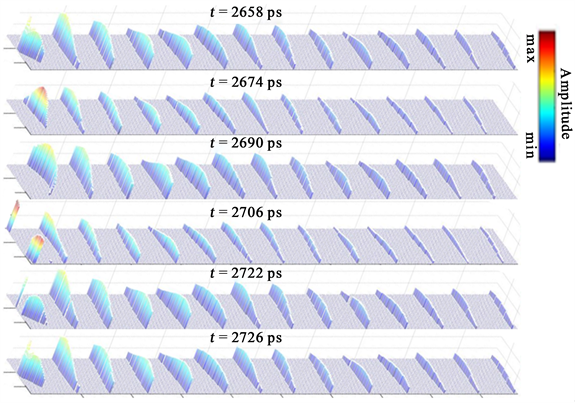
Figure 7. A three-dimensional bar chart of equal phase lines
图7. 等相位线的立体柱状图
下面我们来计算一下携带横向轨道角动量的自旋波的波速。为了计算方便,以t = 2666 ps时画出的等相位线图为例,从摆动场所在的列数开始向右数,第7条等相位线和第14条等相位线的相对于+y方向的偏角均为0˚,在不考虑计算等相位线相对于+y方向的偏角时出现少许误差的情况下,波长λ就等于第7条等相位线和第14条等相位线之间的距离,通过计算,自旋波的波长λ= 510 nm,又因为相邻两条等相位线之间的时间间隔68 ps,因此自旋波的周期T= 68 × 7 = 476 ps,故波速
即,携带横向轨道角动量的自旋波具有较大的波速。
5. 两列携带横向轨道角动量的自旋波在空间的干涉
我们知道,两列不携带横向轨道角动量的平面自旋波在空间相遇时会发生干涉相消或干涉相长的现象,那么,两列带有横向轨道角动量的自旋波在空间相遇时,会有怎样的现象发生呢?下面,我们就来进行详细讨论。依然采用相同的准二维铁磁性纳米条带尺寸,为了在样品中产生两列带有横向轨道角动量的自旋波,考虑到两个摆动场的施加位置关于样品中心位置的对称性,在样品452 nm ≤x≤ 500 nm的范围内和1700 nm ≤x≤ 1748 nm的范围内分别施加两个振幅H均为100 mT,频率f均为14.65 GHz的摆动场。摆动场依然施加在y-z平面内且从−z轴开始并在−z轴和+z轴之间来回连续摆动。这样一来,连续摆动的摆动场产生的两列携带横向轨道角动量的自旋波将会在900 nm ≤x≤ 1300 nm区域内相遇并发生干涉。不同时刻两列自旋波的波形如图8所示。

Figure8. Interference of Two Spin Waves Carrying Transverse Orbital Angular Momentum in Space
图8. 两列携带横向轨道角动量的自旋波在空间的干涉
由于分别沿−x和+x方向传播的两列自旋波所携带的横向轨道角动量符号相反,在干涉区域内叠加后变成了平面波!把发生干涉的区域总长度分别扩大到800 nm和1200 nm后,仍然观察到类似的现象。这说明,自旋波的等相位面发生弯曲不是由于波与样品上下边缘反射所引起的,而是摆动磁场导致自旋波携带横向轨道角动量。
6. 总结
我们对一个准二维坡莫合金准二维坡莫合金纳米条带施加摆动磁场,通过对样品磁矩振动的傅里叶分析,发现了三个携带横向轨道角动量的自旋波模式。在本征频率的连续摆动磁场激发下,我们观察到自旋波传播过程中等相位面在样品平面内发生幅度约正、负5度的转动。由于磁子沿S形弯曲轨迹运动,自旋波携带的轨道角动量垂直于样品表面,也与波的传播方向垂直。这种横向轨道角动量的方向在每半个波长发生一次翻转。即由垂直样品面朝上转为朝下,或者相反。我们还探索了两列携带横向轨道角动量的自旋波在纳米条带中相向传播时发生的干涉现象。当两列波叠加时携带的横向轨道角动量符号相反,就产生不带角动量的平面自旋波。我们的研究发现了准二维磁性体系中携带横向轨道角动量的自旋波模式,为自旋波的动力学研究开辟了一个新窗口。