1. 引言
高超速飞行器是一种飞行Mach数大于5的临近空间飞行的飞行器,是武器技术发展中的一个重要里程碑,其具体应用形式包括高超声速巡航导弹、高超声速有人/无人飞机、空天飞机和空天导弹等多种飞行器 [1] 。当各类高超速飞行器在大气层内飞行时,周围空气受到弓形激波的强烈压缩,与飞行器表面产生强烈的摩擦作用,致使空气温度急剧上升。在飞行器表面与高温空气相互作用的过程中,部分热能通过边界层传递给飞行器表面,这一现象被称为“气动加热” [2] 。影响高超速飞行器在边界层内传热的因素较多,并且相互影响,要想实现气动热精确的预测十分困难。为了能够在飞行过程中感知外部环境,常利用结构内部的温度、应变等信息反演获得飞行器气动力和气动热参数。因此,能够准确预测气动加热过程中的温度场分布,是开展飞行器气动力、气动热参数辨识的基础,同时有利于改进飞行器结构设计、实现飞行器的安全飞行 [3] 。
针对高速飞行器的气动加热过程,研究人员分别从理论、实验以及数值模拟方面展开了大量研究,其主要是从飞行器飞行试验的遥测、外测等诸多实验数据中辨识出飞行器的气动力、气动热参数。利用热流耦合分析的方法,Zhang等人 [4] 针对高超声速环境中钝锥的气动加热特性进行了理论分析,所得结果与使用热电偶测量的数据吻合较好。张超等 [5] 利用ANSYS软件,建立了完整的热流辨识的数值求解方法,验证了ANSYS软件可以有效求解气动加热问题,并对流场、温度场、结构场特性进行了数值分析研究。Huo等人 [6] 利用修正牛顿理论建立了高超声速飞行器工程气动加热快速计算方法,获得了飞行器表面的压力分布,同时利用参考焓法求出了表面的热流密度。可见,气动热参数辨识是一个基于结果求原因的“热传导反问题” [7] 。然而,为了获得较为准确的预测,对于正问题的求解至关重要。于是,本文为进一步开展气动热参数识别提供理论基础,将高速飞行器的气动加热过程简化为受热流边界的物理模型,利用热传导的基本理论获得结构内部温度的变化规律。该问题是在已知热物性参数和定解条件的情况下,确定物体的温度分布。热传导正问题的解析解可以用来分析热传导反问题,也可以为实际工程问题的解决提供理论依据 [8] 。
目前,求解热传导方程的方法有很多,如分离变量法、积分变换法、叠加法和正交展开法等,其中分离变量法和积分变换法为解析解求解方法,而近似分析法和数值法为近似解求解方法 [9] 。近似方法的精度不易估计,除非将其结果与解析解作对比。因此,获得结果内部温度分布的解析解显得十分重要。然而,选择使用分离变量法求解时,边界条件要为齐次边界 [10] 。本文通过巧妙处理,建立了热流边界条件下的无限大平板的热传导正问题,并通过分离变量法获得了这一齐次边界条件定解问题的解析解。通过编写MATLAB程序对热流边界条件下的解析解进行求解,并与有限元仿真结果进行对比分析。
2. 问题的提出及模型建立
我们将受热流作用的飞行器结构内部温度分布问题,视为一无限大平板受热流边界作用,计算其内部温度分布。也就是,在初始条件时,向一侧壁面施加均匀分布的瞬态热流,获得无限大平板温度分布。针对该问题,我们建立如图1所示的物理模型,在结构的左侧边界受到均匀分布的瞬态热流场q(t)。我们取平板的厚度为lmm,平板的左侧与y轴重合;通过分析获得平板内任意一点任意一时刻的温度u(x,t)。
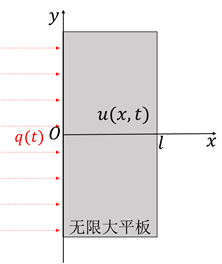
Figure 1. An analytical model for heat conduction problem with heat flux boundary condition
图1. 已知热流边界条件热传导问题的分析模型
根据传热学相关理论,可得该问题的控制方程和边界条件为: [11]
(1)
式中
,D为热扩散率或热扩散系数,
为平板的密度,单位为kg/m3;c为平板的比热容,单位为为J/(kg∙K);k为平板的传热系数,单位为W/(m∙K);
为温度函数
关于时间的一阶导数;
为
关于x的二阶导数;
为热流函数。
3. 求解过程
为了获得上述问题的解析解,我们采用分离变量法对式(1)所述的问题进行求解。考虑到上述问题的边界条件为非齐次边界,于是我们引入新的未知函数
和辅助函数
,并使
满足原未知函数
所具有的非齐次边界条件,则对于新的未知函数
而言,其边界条件便可实现齐次化 [12] 。即令
(2)
其中,
(3)
其中,
为一待定函数,通过选择合适的
,可使得关于
的控制方程和边界条件为其次的。为此,将式(2)带入待定问题式(1)可得,
(4)
为使关于
的控制方程和边界条件是齐次的,即,
(5)
只需求解
的二阶常微分方程的边值问题,
(6)
综上,式(1)所描述的问题将转化为求解式(5)和(6)的两个问题。
(a) (6)式的通解为:
(7)
其中
,
。
(b) 利用分离变量法可得公式(5)的解为:
(8)
其中,
(9)
(10)
将(3)、(7)、(8)式代入(2)式整理可得
的解为:
1) 当
时
(11)
其中,
(12)
(13)
2) 当
时
(14)
其中,
(15)
(16)
3) 当
时,
(17)
4. 结果分析
接下来,基于MATLAB程序将上述正问题的理论求解过程进行计算,同时与COMSOL有限元仿真结果进行对比分析。COMSOL有限元仿真时选择固体传热模块,建立与理论分析相同的物理模型,左侧边界为热通量边界,其余为热绝缘边界。由于采取内置模块进行分析,本文便不对其进行详细阐述。本文分别选取三种不同密度、比热容和热导率的无限大平板进行理论计算,具体参数设置如表1所示。

Table 1. Influencing factors of heat flow boundary conditions
表1. 热流边界条件下各影响因素列表
首先,我们选取边界热流密度随时间指数增加的情形进行分析。热流密度随时间变化的函数关系为:
,随时间变化的曲线如图2所示,可以看出热流密度随时间逐渐增加几乎呈线性增加。通过理论分析与有限元分析,我们均提取无限大平板模型中轴线距离表面0.01 mm位置处的温度进行对比分析。
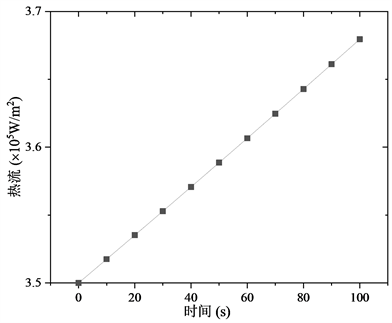
Figure 2. Heat flow exponentially varies with time
图2. 随时间指数变化的热流
图3为不同热物性参数条件下,经受指数热流变化结构温度变化的理论计算与有限元仿真结果。由图3(a)可知,不同比热容条件下,温度随时间线性增加;比热容越大,增加的斜率越小。理论与仿真之间的误差的绝对值的最大值分别为0.34,0.33和0.32 K。从图3(b)可知,结构的温度随时间上升的斜率与密度呈反相关的变化趋势,结构的密度越大,相同时间内温度的变化值较小;在密度分别为7000,8000和9000 kg/m3时,绝对误差的最大值分别为0.35,0.34和0.32 K。对于以上两种条件下的温度变化,可以用热力学中的比热容公式解释,即
,其中q为热流,c为比热容,m为质量,V为体积,ρ 为密度,
为温度随时间的变化率。当热流和质量一定时,比热容c和温度随时间的变化率
成反比,即比热容越大温度随时间的变化率越小;当热流、比热容和体积一定时,密度ρ和温度随时间的变化率
成反相关,即密度越大温度随时间的变化率越小。而针对三种热导率的结构而言,每一种结构的温度上升趋势基本一致,差异不大(图3(c));理论与仿真之间的绝对误差的最大值小于0.41 K;当时间超过2 s后,绝对误差不大于0.004 K。可以看出,通过分离变量法获得的温度分布与有限元仿真结果基本一致,验证了理论分析结果的准确性。
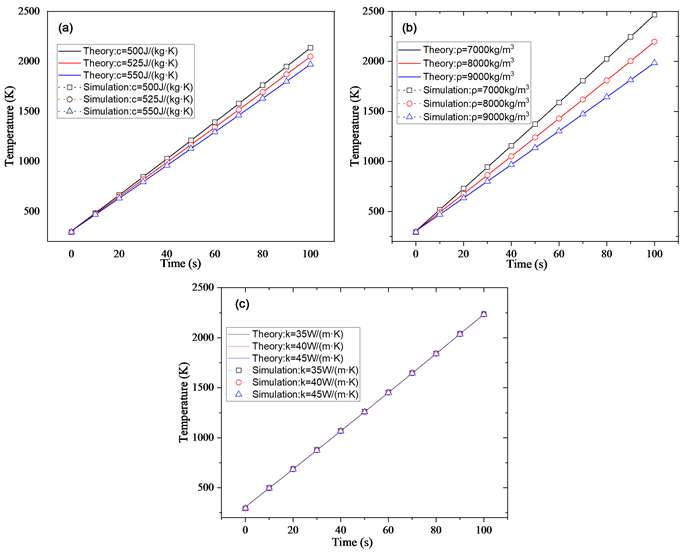
Figure 3. Comparison of temperature change with time under different thermophysical property parameters: (a) specific heat capacity; (b) density; (c) thermal conductivity
图3. 不同热物性参数下温度随时间变化关系的比较:(a) 比热容;(b) 密度;(c) 热导率
为了使得所推导的理论结果更具有一般性,我们选取了结构边界热流随时间阶跃变化的形式,其热流变化如图4所示。在初始阶段,结构的热流为0,随着时间的推移,热流密度突然增加为3 × 105W/m2,保持一段时间后,增加至8 × 105W/m2。
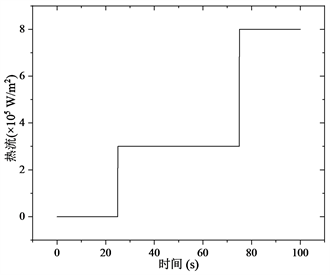
Figure 4. Step change of heat flow with time
图4. 随时间按阶跃变化的热流
图5为不同热物性参数条件下,热流密度随时间阶跃变化下,结构内部温度随时间变化关系的理论计算与有限元仿真结果。可以看出,当温度发生突变时,结构的温度也随之发生突变。在0~25 s时间段,由于此时热流密度为零,因此结构的温度也保持不变;在25 s~75 s时间段和75 s~100 s时间段,温度随时间线性增加,且比热容越大,增加的斜率越小。
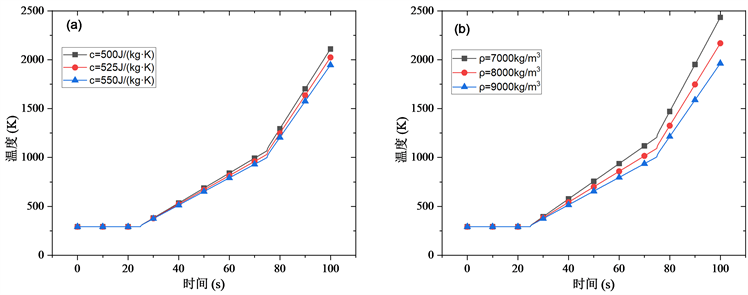
Figure 5. Temperature change with time under different thermophysical property parameters: (a) specific heat capacity; (b) density
图5. 不同热物性参数下温度随时间变化关系的比较:(a) 比热容;(b) 密度
5. 结论
本文将超高速飞行器在运行过程中受热流作用下的温度变化视为热流边界下无限大平板的热传导问题,建立了热流边界条件激励下的传热问题,并通过分离变量法获得了非齐次边界条件定解问题的解析解。通过对不同热流分布形式下结构温度场的理论分析结果与有限元结果分析对比表明,本文利用分离变化量法获得的温度分布与模拟结果吻合较好,并且能够对指数变化、梯度变化等多种形式的热流变化所引起的温度变化能够做出预测,绝对误差最大值发生在初始2 s内,不超过0.5 K;时间超过2 s后,理论与有限元仿真计算结果的绝对误差不超过0.005 K。相关结果能够为进一步开展热流辨识以及结构受热分析等提供理论基础。