1. 引言
低轨(Low Earth Orbit, LEO)卫星星座因其低传输时延、低功耗链路等优点,在现代移动通信领域发挥着重要的作用。为了提高卫星网络的灵活性与适应性,低轨卫星通常采用多波束技术,并逐渐采用全频率复用方案来充分利用稀缺的频谱资源、提高通信系统的容量。然而,全频率复用不可避免地导致了波束间干扰的增强 [1] 。同时,低轨卫星经常部署在倾斜轨道和极地轨道,当多个卫星同时运行经过高纬地区,它们的波束会产生过高的重叠;当低轨卫星经过沙漠、海洋等通信需求较少的地区时,如果保持波束开启,会导致功率的浪费。这些均是星上资源的无效利用。故目前实际运行的低轨卫星星座大多采用波束关闭算法来减少波束资源的开销,进而降低星上功率,减少波束间相互干扰,提升通信质量。
近年来,卫星波束开关算法被广泛研究。例如,文献 [2] 提出了一种基于用户位置的低轨卫星动态波束关闭算法,其核心是计算每个服务用户是否被卫星波束覆盖,基于此对波束进行关闭,以此节约波束资源。文献 [3] 提出了预规划服务单元波束分配算法(PSBA)和动态服务单元波束分配算法(DSBA),该算法在波束资源的规划中考虑了卫星视距内蜂窝服务的情况。但是,由于文献 [2] 的方法考虑的是单个用户,其复杂度会随用户规模的增大而快速增加,同时每次服务区域切换时都需要执行算法来调整部分波束的开关情况,无法满足低轨卫星通信的实时性要求。同时,文献 [2] 和文献 [3] 只考虑地面业务的需求,没有考虑卫星星座视场下波束信号强度对通信性能的影响。文献 [4] 提出的动态波束关闭算法基于波束重叠覆盖情况来调整冗余的波束。但是,该算法仅考虑了波束重叠层数,没有精细到波束信号强度,导致波束真实覆盖范围内实际存在的信号盲区被忽略;并且业务需求只考虑了人口分布,没有具体考虑业务需求。
基于上述的分析,本文采用通信业务量代替原来的用户个人需求来降低算法复杂度,同时考虑用波束信号强度代替波束重叠层数,还原实际波束覆盖下存在的信号盲区,这样在保证用户服务质量的同时,降低了大规模用户情况下的算法复杂度。此外,通信业务量的分布与人类生产活动紧密相关,呈现出明显的周期性 [5] ,对它的精确预测对于合理分配通信资源具有重要的意义。现有研究利用了乘积季节自回归求和移动平均(S-ARIMA)模型 [6] 、模糊时间序列模型 [7] 等时间序列模型对通信业务量进行预测。但因为通信业务量分布不仅具有时间相关性,还具有空间相关性,所以仅使用时间序列预测模型很难提取数据的空间特征,而空间相关性的缺失会造成预测结果的不准确 [8] 。因此,在本文中利用了卷积长短期记忆神经网络(Conv-LSTM)来对通信业务量进行预测,它能同时提取数据的时间和空间特性,适用于这类短时的业务预测问题。并且,根据通信业务量预测的结果,可以在低轨卫星切换服务区域时,提前获知下一个区域的业务量分布情况,从而对波束的开关状态进行预设,有效减少了服务区域切换时波束调整的次数。
因此,本文基于神经网络预测的地面通信业务量分布和波束信号强度的仿真,提出了低轨卫星波束动态开关算法,综合考虑了波束覆盖区域的信号盲区与地面通信业务量,有效节约重叠的波束资源,减少波束调整次数,降低大规模情况的算法复杂度。
2. 系统模型
2.1. 低轨卫星星座场景描述
将低轨卫星星座系统的卫星个数记作
,星座内卫星依次可表示为
。每颗卫星的波束个数记作
,
表示卫星
的第j个波束,则系统总波束个数为
。
终端–波束相关的覆盖因子:
卫星各波束采用圆波束模型,对应的波束角(BW, Beam Width)记为
。对于波束
、终端
而言,当卫星终端指向与波束指向之间的空间夹角小于该波束半波宽时,认为终端被该波束覆盖,否则认为该终端不在波束覆盖范围内。由此,定义终端−波束覆盖因子
,表征终端
是否被波束
覆盖,其表达式为:
(1)
波束激活与否因子:
定义波束激活与否因子
,以表征波束处于激活或关闭状态,其表达式为:
(2)
2.2. 波束资源调度的最优化模型
优化目标 最小化星座网络工作的波束数。
约束条件 当星座网络内要部分波束关闭时,应保证服务区域的覆盖,即在若干波束关闭的情况下,对于服务区域内任意终端而言,至少存在一个激活的波束可覆盖该终端。故动态波束开关最优化问题可以写为:
(3)
其中系统的卫星个数记作
,每颗卫星的波束个数记作
,
表示第i颗卫星的第j个波束激活因子,
表明该波束处于激活状态。
为星座网络覆盖区域内所有用户集合(用户总数为K),
表示终端k与第i颗卫星的第j个波束的覆盖因子,
表明该波束覆盖了终端k。
上述建立的最优化问题属于二重求和问题,目标是最小化激活波束个数,而约束需保证连续覆盖与有业务传输波束不关闭。由此,可将二重求和转化为以波束为基的一重求和问题。设所用卫星的波束数量总和为
,构造波束与终端相关的覆盖矩阵
,其中
记为矩阵
的第n行向量,代表第n个波束的覆盖信息。该覆盖矩阵满足:
(4)
其中
表示矩阵
的第n行、第k列元素。
设所有行向量组成集合
,则优化问题可简化为:
(5)
注:
表示集合中元素的个数。
该优化问题为NP完全问题,很难直接求解 [9] ,因此采用启发式算法。
具体而言,为度量波束开关标准,首先对天线波束方向强度分布进行仿真计算,然后进行动态网络划分,利用Conv-LSTM对各地块通信业务量进行预测,结合两者定义衡量波束业务的重要程度的变量,以此为依据选择需调整的波束,在保证覆盖前提下,优先选择业务更重要的波束,从而得到波束开关的次优解。
3. 波束信号强度分析
本小节主要通过阵列天线波束赋形原理,将其信号强度映射到经纬度平面坐标中,求得地面波束信号强度分布。
3.1. 卫星本体坐标
如图1所示,卫星本体坐标以卫星平台质心为坐标原点O,以原点指向地心为正z轴,以原点O指向卫星切线运行方向为正x轴,根据右手法则得到y轴。对于波束
,在卫星
本体坐标系下,定义其空间指向
。其中,方位角
定义为以正x轴顺时针方向到波束指向在xOy平面投影的角度,仰角
定义为波束指向与xOz平面的夹角。卫星指向终端
的方向为
。由空间对应关系可知,空间向量
对应的Oxyz表示
为:
(6)
且
同理可得。
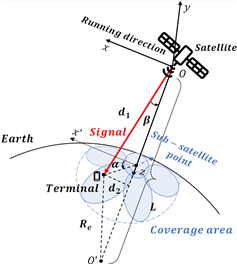
Figure 1. Satellite ontology coordinate system
图1. 卫星本体坐标
3.2. 波束赋形
在多天线系统中,一般将二维平面阵列天线认为是远场平面波传输。假设为均匀间距的二维面阵,阵元数为
,其中N为x轴方向上的阵元数,M为y轴方向上的阵元数,相邻阵元间隔为d。阵面平面直角坐标系的坐标原点设置在第
阵元处。
定义天线阵列直角坐标系中的两个角度,如图2所示,其中
,为波束指向投影到yOz平面
与y轴的夹角,
为波束指向投影到xOz平面与x轴的夹角。则它们与方位角
、仰角
的转化公式如下:

Figure 2. Antenna and satellite coordinates
图2. 天线坐标与卫星本体坐标
(7)
利用阵列天线球面坐标可得天线阵列单元方向矢量
:
(8)
以及权值矢量,即相控阵天线的48组波束指向
决定的波束方向权重
:
(9)
则均匀阵列天线的方向图函数表达式为:
(10)
将三维空间的48个波束方向矢量图
叠加,所得结果投影到经纬度平面坐标中,将该图样定义为单颗卫星覆盖范围内的波束强度分布
,如图3所示。

Figure 3. Diagram of beam signal strength distribution
图3. 波束信号强度分布
4. 基于卷积长短期记忆神经网络(Conv-LSTM)的通信业务量预测
本小节主要通过Conv-LSTM对地面通信业务量进行时空预测,输出得到地面业务密度分布图,并对其MAPE进行仿真,以此衡量预测效果。
4.1. 通信业务量
通信业务量是指在通信网络中传输的各类信息所包含的总信息量。若某线路有m条信道,第i信道被占用
秒,则该线路上的业务量Q为:
(11)
单位时间内的通信业务量M通常称为呼叫量,定义为观测时间内的通信业务量Q与观测时间T的比值,其单位为小时呼或爱尔兰(Erlang),即:
(12)
4.2. 业务密度
定义网格单元内的通信业务量为业务密度
,单位为Erlang/m2。故第n个波束覆盖下的第x行、第y列网格单元的业务密度为:
(13)
其中
表示业务i的平均达到率,
表示业务i的平均服务时长,
表示当前网格单元的业务i的总业务量,
表示单位网格的面积 [10] 。
4.3. 卷积神经网络架构
Conv-LSTM是基于长短期记忆神经网络(LSTM)发展而来的、用于解决时空序列预测问题的神经网络 [11] 。在Conv-LSTM的架构中,输入是一组时空序列数据,而其输入与状态、状态间均由卷积运算连接而不是全连接,这是Conv-LSTM与时间序列预测模型最大的不同之处,也是Conv-LSTM能捕捉空间相关性的原因。网络的输出则由网络层构决定的。
通常,Conv-LSTM的输入是一组连续时刻的图片。输入前先利用聚类算法对图片进行降噪处理,再将图片划分为一个由M行N列组成的网格图。在每个网格单元中,有P个测量值随时间而变化。故任何时刻的观测值都可以用张量
表示,其中
表示观测特征的域。因此,Conv-LSTM的输入实际是一个3D张量。假设预测未来k个序列,则预测序列可以通过将之前的J次观测数据输入网络得到:
(14)
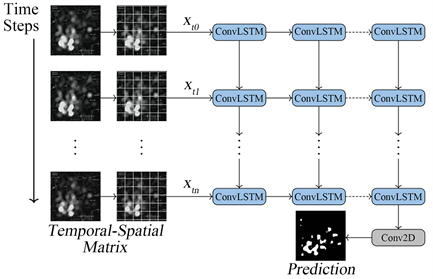
Figure 4. Diagram of Conv-LSTM Network layer
图4. Conv-LSTM网络层构
Conv-LSTM的网络层构如图4所示。输入是一组连续时刻的业务量分布热力图,每张图经过一个两层Conv-LSTM构成的Encoder网络和一层Conv-LSTM构成的Decoder层,其中Decoder层的输入是从Encoder层的输出copy而来。最后将网络输出通过Conv2D层并进行二值化获得预测结果。
Conv-LSTM的cell结构为:
(15)
预测网络通常的网络层构为Encoder-Decoder结构,这样可以使得神经网络的输出是与输入相同大小的图片,并定义该网络二值化的输出结果为预测的业务量
。虽然预测长度为K个序列的计算复杂度可以达到
,但在实际问题中,可以利用预测空间的结构来降低维数,从而使问题易于处理。
4.4. 平均绝对百分比误差
本文采用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)来衡量Conv-LSTM神经网络在预测通信业务量方面的效果,其定义为:
(16)
其中,N为样本个数,
为实际值,
为预测值。
实验所得的MAPE为13.87%,说明Conv-LSTM能较好的预测通信业务量。
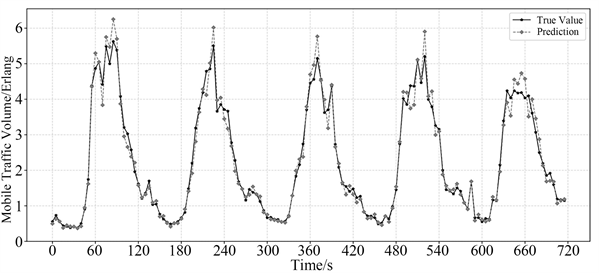
Figure 5. Comparison of the values of Conv-LSTM between predicted and true values
图5. Conv-LSTM预测值与真实值对比
图5是在仿真时间内,某地点的通信业务量的预测值和真实值的对比。图像的横坐标表示仿真时间,纵坐标表示通信业务量。
5. 波束动态开关算法实现
5.1. 波束业务重要程度
由转化所得的优化问题B可知,需在满足约束条件的同时选择尽可能多的冗余波束将其关闭。基于前文关于通信业务量预测和波束强度仿真的工作,可以进一步定义波束关闭的衡量条件,即波束业务重要程度。
定义以下变量:
A. 单位网格业务密度
:该变量参数为神经网络预测的结果。
B. 单位网格信号强度
:该变量参数为相控阵天线波束方向强度仿真结果。
C. 单位网格业务重要程度定义为:单位网格业务密度与单位网格信号强度的比值。
(17)
D. 第n个波束业务重要程度定义为:先将该波束n覆盖区域内的
叠加,再与网格数
之比。
(18)
图6是基于网格划分的业务重要程度分布,将单个波束覆盖范围内的所有网格的业务重要程度求均值,即可得第n个波束的业务重要程度
:

Figure 6. Diagram of the distribution of business importance
图6. 业务重要程度分布图
该图是将通信业务量分布图和信号强度分布图均匀划分为128 × 128的网格图,即
,并根
据业务重要程度公式
计算获得每个网格的业务重要程度。
波束方向强度和业务量定义衡量波束业务的重要程度的变量,以此选择需调整的波束,在保证全覆盖前提下,优先选择业务更重要的波束,从而得到波束开关的次优解。
5.2. 算法过程
波束关闭原则:
原则1 重叠更严重的波束应优先关闭。对波束而言,业务量密度小的波束更应该被关闭。对该波束所覆盖的终端而言,总波束信号强度更大的将被优先关闭。
原则2 关闭后导致约束条件不再满足的波束不应被选择。
6. 仿真与结果分析
6.1. 仿真场景及参数设置
本次仿真数据集采用的是米兰(MILAN)数据集。该数据集由米兰市在2013年11月1日至2014年1月1日期间汇总的电信数据组成。电信数据包括接收短信、发送短信、来电、去电和互联网的汇总信息活动,并通过呼叫详细记录(CDR)来衡量,其通信业务量单位为爱尔兰(Erlang)。数据按小时汇总,并列在城市内300平方千米的区域内。城市被划分为640 × 640的网格,并用一个二进制邻接矩阵来表示城市中网格之间的连通性。我们采用其中用户连接请求的数据将其制成的二维热力图,再对其进行灰度转化。
利用MATLAB作为仿真平台,部署66颗卫星,每个卫星有48个波束,分别比较基于用户位置和基于波束业务重要的波束动态开关算法下波束开启数量和波束调整次数。系统参数如表1所示,总仿真时长为7200 s。

Table 1. System resulting data of standard experiment
表1. 标准试验系统结果数据
6.2. 仿真分析
仿真采用同一时段的通信业务量数据与预测结果,除了使用的关闭策略不同,其余参数相同。由图7可知,在同一卫星的相同运行过程中,基于业务重要程度的算法可节约与基于用户位置的算法几乎相同的波束资源,同时基于业务重要程度的算法由于采用了固定大小的网格代替接入服务的用户,因此在用户数量增加时,算法所需时间要明显少于基于用户位置的算法。这说明计算复杂度在服务的用户数量增幅较大时增长得更平缓。

Figure 7. Comparison of the number of activated beams under different constraints
图7. 不同约束条件下波束开启数量对比
图8是不同约束条件下波束调整次数对比。仿真采用两种算法各自连续执行一段时间,对比利用基于覆盖程度和基于业务重要程度的算法在减少波束调整次数的作用。从图中看出业务重要程度的引入可有效减少服务区域切换时的波束调整次数,且无需在每个新时刻重新执行算法,降低了算法的功耗。

Figure 8. Comparison of beam adjustment times of satellite during service region switching under different constraints
图8. 不同约束条件下波束调整次数对比
7. 总结
本文提出的基于业务量预测的低轨卫星波束动态开关算法,相较于传统的波束动态开关算法,具有以下优点:首先,算法利用波束业务重要程度控制,综合考虑波束信号强度与通信业务供需两方面因素,考虑了实际波束覆盖区域中的信号盲区,可有效减少高纬地区的波束资源浪费和中低纬地区的波束重叠覆盖、乒乓切换等问题。同时,可调的业务重要程度门限保证了在高动态下的算法快速收敛性;并且,算法利用网格划分法将单个用户的通信需求转化为网格内用户群的通信业务量,可有效控制矩阵的规模,降低大规模用户时算法复杂度,适用于低轨卫星星座这一通信场景。此外,利用Conv-LSTM对通信业务量热力图进行时空序列预测,获得较为精确的未来通信业务量分布,并根据所预测的业务量分布预先对卫星的波束开关进行设置,有效减少了波束的调整次数。
基金项目
本项目获得东南大学大学生创新创业训练项目资金支持。