DOI:10.12677/DSC.2023.123015,PDF,HTML,XML,被引量下载: 378浏览: 973科研立项经费支持
作者:何 鑫,严 芳,赵红霞,贾亚琪,张春梅：重庆理工大学理学院，重庆
关键词:无限状态马尔可夫跳跃系统；黎卡提方程；离散时间；H∞控制；Infinite State Markov Jump System；Riccati Equation；Discrete Time；H∞ Control

文章引用：何鑫, 严芳, 赵红霞, 贾亚琪, 张春梅. 一类离散时间无限状态马尔可夫跳跃系统H∞控制[J]. 动力系统与控制, 2023, 12(3): 139-148. https://doi.org/10.12677/DSC.2023.123015

1. 引言

马尔科夫跳跃系统是一类常见的随机系统，它常用于描述存在突变因素的系统，例如金融经济、管理科学、飞机控制等。而对于随机系统的一个热点研究方向是控制器的设定，而H_∞控制理论是控制理论中重要的鲁棒控制设计方法，因为它的工程应用是为了去消除独立外部输入扰动 $v\left(t\right)$的影响，所以它能保证控制系统的稳定性。目前针对马尔科夫跳跃系统的H_∞控制的成果有很多，文献 [1] 研究了离散时间广义马尔可夫跳跃系统的随机稳定性和鲁棒控制，文献 [2] 研究了一类具有时变时滞不确定马尔可夫跳变线性系统的鲁棒输出反馈H_∞控制。文献 [3] 研究了周期马尔科夫跳变系统的H_∞滤波问题；文献 [4] 研究了一类离散时间马尔可夫跳变系统在状态和控制变量约束下的二次型最优控制问题。文献 [5] [6] 研究了一类具有随机突变和未知的转移概率，但在每种模式的已知界限之间变化的离散时间线性系统，重新讨论了这类系统的H_∞控制问题。

带马尔科夫和乘性噪声的随机系统是一类特殊的随机系统，近些年针对它的研究也有很多，文献 [7] 讨论了在方差约束下带马尔科夫和乘性噪声的随机系统的鲁棒控制问题，给出了具有方差约束的鲁棒控制器设计方法。文献 [8] 研究了一个具有白噪声扰动和马尔可夫跳变的随机系统的N个参和者的最优控制问题。文献 [9] 针对某些系统在一定的采样间隔内转移概率不变或者变化缓慢的情况，提出了分段带乘性噪声的齐次离散时间Markov跳跃系统模型，并研究了系统H_∞估计问题。文献 [10] 研究了具有乘性噪声和马尔可夫链的部分观测值的马尔可夫跳跃线性系统的控制问题。文献 [11] 针对一类带乘性噪声的离散时间不确定奇异随机马尔可夫跳跃系统，研究了异步输出H_∞反馈控制问题。

上述文献主要讨论的是有限时域或者有限状态的Markov跳跃系统的H_∞控制问题。而文献 [12] 研究了一类具有无限马尔可夫跳变和乘性噪声的离散时滞随机系统的控制问题。文献 [13] [14] 中提出了一个随机版本的有界实引理。受上述文献的启发，本文将文献 [13] 的有界实引理推广到具有无限马尔可夫跳变参数和乘性噪声的无限时域离散时间时变系统，然后应用到H_∞控制问题。

本文主要研究了在状态反馈控制器设计情况下探寻闭环系统的稳定性和H_∞控制问题，得到了代数黎卡提方程稳定解与系统内部稳定性、线性矩阵不等式之间的等价性。首先介绍了所考虑系统的一些预备知识，比如系统的指数均方稳定性、扰动算子的定义以及舒尔补引理。然后利用舒尔补引理得到线性矩阵不等式、黎卡提方程稳定解的等价性、系统内部均方稳定性之间的等价性。

2. 预备知识与模型描述

本小节首先给出常用符号说明；其次简单介绍马尔可夫链相关的定义和随机系统中常用的稳定性定理；最后提供主要的数学引理。

本文中， $R^n$表示n维欧氏空间； $R^{n\times m}$表示 $n\times m$实矩阵线性空间， $\Vert ·\Vert$表示 $R^n$欧氏范数或者 $R^{m\times n}$算子范数， $S_n$表示n阶对称矩阵； $A^T$表示矩阵(向量) A的转置， $A>0\left(A\ge 0\right)$表示A是正定(半正定)；记 $I=\left(I_n,I_n,\cdots \right)$， $I_n$表示n阶恒等矩阵， $S=\left\{1,2,\cdots \right\}$， $D=\left\{1,2,\cdots \right\}$， $Z_{+}=\left\{0,1,2,\cdots \right\}$； $AN\ast$等价于 $AN{A}^T$， $A\ast$等价于 $A{A}^T$，特别的

$\left(\begin{array}{cc}A& B\\ B^T& C\end{array}\right)=\left(\begin{array}{cc}A& B\\ \ast & C\end{array}\right)$,

$\ast$表示对称项； $\gg$表示一致正， $\sigma \left(A\right)$表示由A生成的最小 $\sigma$代数， $\Omega$表示样本空间， $P(·)$表示事件发生的概率， $P\left(A|B\right)$表示给定事件B情形下事件A发生的条件概率， $E\left[A\right]$表示事件A发生的数学期望， $E\left[\cdot |A\right]$表示关于事件A发生的条件期望。

在给定完备概率空间 $\left(\Omega ,\mathcal{H},P\right)$中，考虑带有无限马尔可夫跳参数、乘性噪声和独立外部输入扰动的离散随机系统如下：

$\begin{array}{l}x\left(t+1\right)=\left[A_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{A}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]x\left(t\right)+\left[B_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{B}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]u\left(t\right)\\ +\left[M_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{M}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]v\left(t\right)\\ z\left(t\right)=C\left({\eta }_t\right)x\left(t\right)+D\left({\eta }_t\right)u\left(t\right)+G\left({\eta }_t\right)v\left(t\right)\end{array}$(1)

$x\left(t\right)\in R^n,u\left(t\right)\in R^{n_u},v\left(t\right)\in R^{n_v},z\left(t\right)\in R^{n_z}$分别表示系统状态、外部控制、外部扰动输入、控制输出。 ${\left\{A_k\left({\eta }_t\right)\right\}}_t,{\left\{B_k\left({\eta }_t\right)\right\}}_t,{\left\{C\left({\eta }_t\right)\right\}}_t,{\left\{D\left({\eta }_t\right)\right\}}_t,{\left\{G\left({\eta }_t\right)\right\}}_t,{\left\{M_k\left({\eta }_t\right)\right\}}_t$都是具有合适维数的实矩阵序列。 $\omega \left(t\right)=\left({\omega }_1\left(t\right),{\omega }_2\left(t\right),\cdots ,{\omega }_r\left(t\right)\right)$是互相独立的随机向量序列，也称为乘性噪声 $E\left[\omega \left(t\right){\omega }^{\text{T}}\left(t\right)\right]=I_r$， $E\left[\omega \left(t\right)\right]=0$。

令 ${\mathcal{H}}_t=\sigma \left\{{\eta }_k,{\omega }_s|0\le k\le t,0\le s\le t-1\right\}$，当 $t=0$时，有 ${\mathcal{H}}_0=\sigma \left({\eta }_0\right)$。 ${\left\{{\eta }_t\right\}}_{t\in Z_{+}}$和 ${\left\{{\omega }_t\right\}}_{t\in Z_{+}}$相互独立。 ${\left\{{\eta }_t\right\}}_{t\in Z_{+}}$是取值于可列可数集S中的马尔可夫链，其切换依赖于一个平稳非退化转移概率矩阵： $\text{P}=\left[p\left(i,j\right)\right]$

$p\left(i,j\right)=P\left\{{\eta }_{t+1}=j|{\eta }_t=i\right\},j\in S$(2)

且具有性质：

$\{\begin{array}{l}p\left(i,j\right)\ge 0,\hfill \\ {\displaystyle \underset{j=1}{\overset{\infty }{\sum }}p\left(i,j\right)=1.}\hfill \end{array}$(3)

记 $l^2\left(0,\infty ;R^m\right)$表示 $R^m$值随机过程 $\left\{y\left(t,\omega \right)\right\}$满足 ${\mathcal{H}}_t$可测和 ${\displaystyle {\sum }_{t=0}^{\infty }E\left({\Vert y_t\Vert }^2\right)}<\infty$的空间，故 $l^2\left(0,\infty ;R^m\right)$是实Hilbert空间，其范数由通常的内积诱导：

${\Vert y\Vert }_{l^2\left(0,\infty ;R^m\right)}^2={\left({\displaystyle {\sum }_{t=0}^{\infty }E\left({\Vert y_t\Vert }^2\right)}\right)}^{1/2}<\infty$.

记 ${\text{H}}_1^{m\times n}$表示集合 $\left\{\text{H}|\text{H}=\left(\text{H}\left(1\right),\text{H}\left(2\right),\cdots \right)\right\}$ $\text{H}\left(i\right)\in R^{m\times n}$这其中 ${\displaystyle {\sum }_{i=1}^{\infty }\Vert \text{H}\left(i\right)\Vert }<\infty$，很容易得到 ${\text{H}}_1^{m\times n}$是具有范数 ${\Vert \text{H}\Vert }_1={\displaystyle {\sum }_{i=1}^{\infty }\Vert \text{H}\left(i\right)\Vert }$的Banach空间；同理定义Banach空间 ${\text{H}}_{\infty }^{m\times n}$，其范数 ${\Vert \text{H}\Vert }_{\infty }=\underset{i\in S}{\sup }\Vert \text{H}\left(i\right)\Vert$。

当 $m=n$， ${\text{H}}_1^{n\times m}\left({\text{H}}_{\infty }^{n\times m}\right)$可简记为 ${\text{H}}_1^n\left({\text{H}}_{\infty }^n\right)$。若 $\text{H}\left(i\right)\in S_n$， $\text{H}\left(i\right)\ge 0$， $i\in S$，用 ${\text{H}}_1^{n+}\left({\text{H}}_{\infty }^{n+}\right)$代替 ${\text{H}}_1^n\left({\text{H}}_{\infty }^n\right)$。对 $X,Y\in {\text{H}}_1^{n+}$， $X\le Y$表示对所有 $X\left(i\right)\le Y\left(i\right)$，且具有性质 ${\Vert X\Vert }_1\le {\Vert Y\Vert }_1$。假设所考虑系统(1)中所有的参数矩阵都具有有限范数 ${\Vert ·\Vert }_{\infty }$， ${\Vert A\Vert }_{\infty }=\underset{i\in S}{\sup }\left\{\Vert A\Vert \right\}<\infty$。此外 $\mathcal{B}\left(\mathcal{X}\right)$表示从 $\mathcal{X}$到 $\mathcal{X}$的所有有界线性算子组成的线性空间。 $\Gamma \in B\left(\mathcal{X}\right)$，它的诱导范数用 ${\Vert \Gamma \Vert }_{\mathcal{X}}$表示。

在后续的研究中，为了公式记法的简便，对 $\forall U\in {\mathrm{H}}_{\infty }^n,F\in {\mathrm{H}}_{\infty }^{m\times n}$我们将运用如下标记：

$\begin{array}{l}{\mathcal{E}}_i\left(U\right)={\displaystyle \underset{j=1}{\overset{\infty }{\sum }}p\left(i,j\right)U\left(j\right)}\\ {\mathcal{L}}_i\left(U\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_k{\left(i\right)}^T{\mathcal{E}}_i\left(U\right)A_k\left(i\right)}\\ {\mathcal{L}}_i^F\left(U\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{\left[A_{kK}\left(i\right)+M_k\left(i\right)F\left(i\right)\right]}^T{\mathcal{E}}_i\left(U\right)\left[A_{kK}\left(i\right)+M_k\left(i\right)F\left(i\right)\right]}\\ {\Pi }_1^i\left(U\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_k{\left(i\right)}^T{\mathcal{E}}_i\left(U\right)A_k\left(i\right)+C{\left(i\right)}^{T}C\left(i\right)}\\ {\Pi }_2^i\left(U\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_k{\left(i\right)}^T{\mathcal{E}}_i\left(U\right)M_k\left(i\right)+C{\left(i\right)}^{T}G\left(i\right)}\\ {\Pi }_3^i\left(U\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{M}_k{\left(i\right)}^T{\mathcal{E}}_i\left(U\right)M_k\left(i\right)}+G{\left(i\right)}^{T}G\left(i\right)-{\gamma }^2{I}_{n_v}\end{array}$(4)

经过直接的计算验证了其中 $\mathcal{E},\mathcal{L}\in B\left({\mathrm{H}}_{\infty }^{n+}\right)$。

首先对于系统(1)的状态控制律定义为： $u\left(t\right)={\rm K}\left({\eta }_t\right)x\left(t\right),K\in {\text{H}}_{\infty }^n$。即上述所考虑的随机系统(1)可改写成如下闭环系统(5)：

$\begin{array}{l}x\left(t+1\right)=\left[\left(A_0\left({\eta }_t\right)+B_0\left({\eta }_t\right)K\left({\eta }_t\right)\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}\left(A_k\left({\eta }_t\right)+B_k\left({\eta }_t\right)K\left({\eta }_t\right)\right){\omega }_k\left(t\right)}\right]x\left(t\right)\\ +\left[M_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{M}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]v\left(t\right)\\ z\left(t\right)=\left[C\left({\eta }_t\right)+D\left({\eta }_t\right)K\left({\eta }_t\right)\right]x\left(t\right)+G\left({\eta }_t\right)v\left(t\right)\end{array}$(5)

为了书写的方便，随机系统(5)可变形为：

$\begin{array}{l}x\left(t+1\right)=\left[A_{0K}\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{A}_{kK}\left({\eta }_t\right){\omega }_k\left(t\right)}\right]x\left(t\right)+\left[M_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{M}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]v\left(t\right)\\ z\left(t\right)=C_K\left({\eta }_t\right)x\left(t\right)+G\left({\eta }_t\right)v\left(t\right)\end{array}$(6)

其中

$A_{kK}\left({\eta }_t\right)=A_k\left({\eta }_t\right)+B_k\left({\eta }_t\right)K\left({\eta }_t\right)$, $C_K=C\left({\eta }_t\right)+D\left({\eta }_t\right)K\left({\eta }_t\right)$,

利用线性系统理论，对闭环系统(5)的解有分解如： $x\left(t\right)=x_{zi}\left(t\right)+x_{zs}\left(t\right)$， $x\left(t\right)$是闭环系统(5)关于初值问题 $x\left(0\right)=x_0$的唯一解。

这里 $x_{zi}=\left\{x_{zi}\left(t\right),t\in Z_{+}\right\}$是以下零输入系统的唯一解，

$\begin{array}{l}{x}_{zi}\left(t+1\right)=\left[A_{0K}\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{A}_{kK}\left({\eta }_t\right){\omega }_k\left(t\right)}\right]x_{zi}\left(t\right)\\ x_{zi}\left(0\right)=x_0\end{array}$(7)

类似的， $x_{zs}=\left\{x_{zs}\left(t\right),t\in Z_{+}\right\}$是以下零初值系统的唯一解，

$\begin{array}{l}{x}_{zs}\left(t+1\right)=\left[A_{0K}\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{A}_{kK}\left({\eta }_t\right){\omega }_k\left(t\right)}\right]x_{zs}\left(t\right)+\left[M_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{M}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]v\left(t\right)\\ x_{zs}\left(0\right)=0\end{array}$(8)

下面是一些关于无限马尔可夫跳系统的基本概念。

定义1 [13] ：如果对任意初值 $\left(x_0,{\eta }_0\right)\in R^n\times S$，都有 $\underset{t\to \infty }{\lim }E\left[{\Vert x_{zi}\left(t\right)\Vert }^2\right]=0$，则称闭环系统(6)是内部均

方稳定，或系统(7)是指数均方稳定(EMSS)。

定义2 [13] ：当系统(6)是指数均方稳定(EMSS)时，定义一个关于系统(6)输入输出扰动线性算子 $\mathcal{T}:l^2\left(0,\infty ;R^{n_v}\right)\to l^2\left(0,\infty ;R^{n_v}\right)$形如：

$\mathcal{T}v\left(t\right)=C_K\left({\eta }_t\right)x_{zs}(t)+G\left({\eta }_t\right)v\left(t\right),t\in Z_{+}$(9)

其中 $v\in l^2\left(0,\infty ;R^m\right)$，当 $v=0$时，意味着所考虑系统(6)没有外部输入扰动，相应的问题也无研究意义；当 $v\ne 0$时，进一步引诱出一个算子范数：

$\Vert \mathcal{T}\Vert =\underset{{\eta }_0\in S,x_0=0}{\sup }\left\{\frac{\Vert \mathcal{T}v\Vert }{\Vert v\Vert };v\in l^2\left(0,\infty ;R^{n_v}\right),\Vert v\Vert \ne 0\right\}$(10)

给定 $\tau \in Z_{+}$，类似的定义另一个算子范数：

${\Vert \mathcal{T}\Vert }_{\tau }=\underset{{\eta }_0\in S,x_0=0}{\sup }\left\{\frac{{\Vert \mathcal{T}v\Vert }_{\tau }}{{\Vert v\Vert }_{\tau }};v\in l^2\left(0,\infty ;R^{n_v}\right),{\Vert v\Vert }_{\tau }\ne 0\right\}$(11)

假设系统(1)中 $u\left(t\right)\equiv 0,v\left(t\right)\equiv 0$，即得到系统(12)如下：

$\begin{array}{l}x\left(t+1\right)=\left[A_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{A}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]x\left(t\right)\\ z\left(t\right)=C\left({\eta }_t\right)x\left(t\right)\end{array}$(12)

定义3 [15] ：如果存在 $c>0$，使得对所有 $k\ge 0$，都有 $f_k\ge cI$，则称 ${\left\{f_k\right\}}_{k\ge 0}$是一致正， $f_k\gg 0$。

引理1 [16] (舒尔补引理)：给定 $U=\left(U\left(1\right),U\left(2\right),\cdots \right)\in {\text{H}}_{\infty }^{n+}$， $V=\left(V\left(1\right),V\left(2\right),\cdots \right)\in {\text{H}}_{\infty }^{n\times m}$， $W=\left(W\left(1\right),W\left(2\right),\cdots \right)\in {\text{H}}_{\infty }^{m+}$。并且 $U^{\text{T}}=U,W^T=W$则下面性质等价。

1) $\left[\begin{array}{cc}U& V\\ \ast & W\end{array}\right]\gg 0$；

2) $U\gg 0$，并且 $W-V^T{U}^{-1}V\gg 0$；

3) $W\gg 0$，并且 $U-V{W}^{-1}{V}^T\gg 0$。

引理2 [13] ：让

$Q\left(\xi ,u\right)={\left(\begin{array}{l}\xi \\ u\end{array}\right)}^T\left(\begin{array}{cc}{Q}_1& Q_2\\ \ast & Q_3\end{array}\right)\left(\begin{array}{l}\xi \\ u\end{array}\right)$(13)

是定义在 $R^{n+m}$上的二次型。如果 $Q_3$是可逆矩阵，则对所有的 $\xi \in R^n,u\in R^m$我们有：

$Q\left(\xi ,u\right)={\xi }^T\left(Q_1-Q_2{Q}_3^{-1}{Q}_2^T\right)\xi +{\left(u+Q_3^{-1}{Q}_2^T\xi \right)}^T{Q}_3\left(u+Q_3^{-1}{Q}_2^T\xi \right)$(14)

3. 主要结果

在给出定理1之前，利用式子(4)，基于系统(5)、(6)我们先给出如下标记：

${\Pi }_{1K}^i\left(X\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_{kK}{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)A_{kK}\left(i\right)}+C_K{\left(i\right)}^T{C}_K\left(i\right)$(15)

${\Pi }_{2K}^i\left(X\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_{kK}{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)M_k\left(i\right)+C_K{\left(i\right)}^{T}G\left(i\right)}$(16)

离散时间随机系统(1)中的控制律定义为 $u\left(t\right)=K\left({\eta }_t\right)x\left(t\right),K\in {\mathrm{H}}_{\infty }^n$

定理1：给定 $\gamma >0$，下面性质等价

1) 闭环系统(5)内部均方稳定，。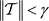

2) 下面代数黎卡提方程有一个稳定解 $X\in {\text{H}}_{\infty }^{n+}$

$\{\begin{array}{l}X\left(i\right)={\Pi }_{1K}^i\left(X\right)-{\Pi }_{2K}^i\left(X\right){\Pi }_3^i{\left(X\right)}^{-1}{\Pi }_{2K}^i{\left(X\right)}^T\\ {\Pi }_3^i\left(X\right)<-{\epsilon }_{0}I,\forall {\epsilon }_0\in \left(0,{\gamma }^2-{\Vert \mathcal{T}\Vert }^2\right),i\in S\end{array}$(17)

3) 这存在一个 $Y\in S_n,Y>0,W\in {\mathrm{H}}_{\infty }^{n+}$对所有的 $i\in S$满足如下线性矩阵不等式(LMI)：

$\left[\begin{array}{cccccc}-Y& Y{A}_0^T\left(i\right)+W^T\left(i\right)B_0^T\left(i\right)& Y{A}_1^T\left(i\right)+W^T\left(i\right)B_1^T\left(i\right)& \cdots & Y{A}_r^T\left(i\right)+W^T\left(i\right)B_r^T\left(i\right)& Y{C}^T\left(i\right)+W^T\left(i\right)D^T\left(i\right)\\ \ast & M_0\left(i\right)M_0{\left(i\right)}^T-Y& M_0\left(i\right)M_1{\left(i\right)}^T& \cdots & M_0\left(i\right)M_r{\left(i\right)}^T& M_0\left(i\right)G{\left(i\right)}^T\\ \ast & \ast & M_1\left(i\right)M_1{\left(i\right)}^{\text{T}}-Y& \cdots & M_1\left(i\right)M_r{\left(i\right)}^T& M_1\left(i\right)G{\left(i\right)}^T\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \ast & \ast & \ast & \cdots & M_r\left(i\right)M_r{\left(i\right)}^T-Y& M_r\left(i\right)G{\left(i\right)}^T\\ \ast & \ast & \ast & \ast & \ast & G\left(i\right)G{\left(i\right)}^T-{\gamma }^2{I}_{n_z}\end{array}\right]$(18)

证明：

1) $\Rightarrow$2)：

已知闭环系统(5)的内部是EMSS，并且 $\Vert \mathcal{T}\Vert <\gamma$。通过文献 [13] 性质8.5，可以推得存在 $X=\left(X\left(1\right),X\left(2\right),\cdots \right)\in H_{\infty }^{n+}$满足下面差分方程(19)：

$\{\begin{array}{l}X\left(i\right)={\Pi }_{1K}^i\left(X\right)-{\Pi }_{2K}^i\left(X\right){\Pi }_3^i{\left(X\right)}^{-1}{\Pi }_{2K}^i{\left(X\right)}^{\text{T}}\\ {\Pi }_3^i\left(X\right)<-{\epsilon }_{0}I,\forall {\epsilon }_0\in \left(0,{\gamma }^2-{\Vert \mathcal{T}\Vert }^2\right),i\in S\end{array}$(19)

接下来只需要证明满足差分方程(19)解的稳定性。给定 $\delta >0$，定义线性扰动算子如式子(20)：

${\mathcal{T}}_{\delta }v\left(t\right)=C_{K\delta }\left({\eta }_t\right)x_{zs}\left(t\right)+G_{\delta }\left({\eta }_t\right)v\left(t\right)$(20)

$x_{zs}\left(t\right)$是系统(6)的零初值解，其中 $C_{K\delta }\left({\eta }_t\right)={\left[C_K{\left({\eta }_t\right)}^T,\delta I\right]}^T$， $G_{\delta }\left({\eta }_t\right)={\left[G{\left({\eta }_t\right)}^T,0\right]}^T$。基于输入输出算子 $\mathcal{T}$的定义，可以推导出对任意充分小的 $\delta >0$，有 $\Vert {\mathcal{T}}_{\delta }\Vert <\lambda$。

同理，存在 $X_{\delta }=\left(X_{\delta }\left(1\right),X_{\delta }\left(2\right),\cdots \right),X_{\delta }\left(i\right)\ge 0,i\in S$满足如下代数黎卡提方程

$\{\begin{array}{l}{X}_{\delta }\left(i\right)={\Pi }_{1K}^i\left(X_{\delta }\right)+{\delta }^{2}I-{\Pi }_{2K}^i\left(X_{\delta }\right){\Pi }_3^i{\left(X_{\delta }\right)}^{-1}{\Pi }_{2K}^i{\left(X_{\delta }\right)}^T\\ {\Pi }_3^i\left(X_{\delta }\right)<-{\epsilon }_{0}I,\forall {\epsilon }_0\in \left(0,{\gamma }^2-{\Vert {\mathcal{T}}_{\delta }\Vert }^2\right),i\in S\end{array}$(21)

利用引理2，通过直接的计算，可以得出存在 $\left\{\Gamma \left({\eta }_t\right)\right\}\in R^{n_u\times n}$使得代数黎卡提方程(17)可以改写成如下方程(22)：

$\begin{array}{l}X\left(i\right)={\left(\begin{array}{c}I\\ \Gamma \left(i\right)\end{array}\right)}^T\left(\begin{array}{cc}{\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_{kK}{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)A_{kK}\left(i\right)}& {\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_{kK}{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)M_k\left(i\right)}\\ \ast & {\displaystyle \underset{k=0}{\overset{r}{\sum }}{M}_k{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)M_k\left(i\right)}\end{array}\right)\ast \\ +{\left(\begin{array}{c}I\\ \Gamma \left(i\right)\end{array}\right)}^T\left(\begin{array}{cc}{C}_K{\left(i\right)}^T{C}_K\left(i\right)& C_K{\left(i\right)}^{\text{T}}G\left(i\right)\\ \ast & G{\left(i\right)}^{\text{T}}G\left(i\right)-{\gamma }^{2}I\end{array}\right)\ast \\ -{\left(\Gamma \left(i\right)-F\left(i\right)\right)}^T\left({\displaystyle \underset{k=0}{\overset{r}{\sum }}{M}_k{\left(i\right)}^T{\mathcal{E}}_i\left(X\right){{\rm M}}_k\left(i\right)}+G^T\left(i\right)G\left(i\right)-{\gamma }^{2}I\right)\ast \end{array}$(22)

其中 $F\left(i\right)=-{\Pi }_3^i{\left(X\right)}^{-1}{\Pi }_{2K}^i{\left(X\right)}^T$。此时，不妨令 $\Gamma \left(i\right)=F\left(i\right)$，则方程(22)可以推得以下方程(23)

$X\left(i\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{\left[A_{kK}\left(i\right)+M_k\left(i\right)F\left(i\right)\right]}^T{\mathcal{E}}_i\left(X\right)\ast }+{\left(C_K\left(i\right)+F\left(i\right)G\left(i\right)\right)}^T\ast$(23)

类似的，方程(21)可以写成方程(24)如下所示：

$\begin{array}{l}{X}_{\delta }\left(i\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{\left[A_{kK}\left(i\right)+M_k\left(i\right)F\left(i\right)\right]}^T{\mathcal{E}}_i\left(X_{\delta }\right)\ast }+{\left(C_K\left(i\right)+F\left(i\right)G\left(i\right)\right)}^T\ast +{\delta }^{2}I\\ -{\left(F\left(i\right)-F^{\delta }\left(i\right)\right)}^T\left[{\displaystyle \underset{k=0}{\overset{r}{\sum }}{M}_k{\left(i\right)}^T{\mathcal{E}}_i\left(X_{\delta }\right)M_k\left(i\right)}+G^T\left(i\right)G\left(i\right)-{\gamma }^{2}I\right]\ast \end{array}$(24)

其中 $F^{\delta }\left(i\right)=-{\Pi }_3^i{\left(X_{\delta }\right)}^{-1}{\Pi }_{2K}^i{\left(X_{\delta }\right)}^T$。联系式子(5)、方程(23)和(24)得到如下等式：

$X_{\delta }\left(i\right)-X\left(i\right)={\mathcal{L}}_i^F\left(X_{\delta }-X\right)+\Delta \left(i\right)$(25)

这里

${\mathcal{L}}_i^F\left(X\right)={\displaystyle \underset{k=0}{\overset{r}{\sum }}{\left[A_{kK}\left(i\right)+M_k\left(i\right)F\left(i\right)\right]}^T{\mathcal{E}}_i\left(X\right)\ast }$

$\Delta \left(i\right)={\delta }^{2}I-{\left[F_i\left(X\right)-F_i^{\delta }\left(X\right)\right]}^T{\Pi }_3^i\left(X_{\delta }\right)\ast$

由上诉证明知 ${\Pi }_3^i\left(X_{\delta }\right)\le -{\epsilon }_{0}I$，故 $\Delta \left(i\right)\ge {\delta }^{2}I$；通过文献 [17] 定理3.2可以推得对所有的 $i\in S$，都有 $X_{\delta }\left(i\right)\ge X\left(i\right)$，由文献 [18] 定理3.2相对应的算子 ${\mathcal{L}}^F$生成指数稳定演化，闭环系统(5)的零解是指数均方稳定EMSS，则对应的代数黎卡提方程(17)的解是稳定解，故2)得证。

接着来证明2) $\Rightarrow$1)：

假设代数黎卡提方程(17)稳定解为 $X\in {\mathrm{H}}_{\infty }^{n+}$，相对应有一个稳定反馈增益 $F\left(i\right)=-{\Pi }_3^i{\left(X\right)}^{-1}{\Pi }_{2K}^i{\left(X\right)}^{\text{T}}$。利用引理1的舒尔补技巧，代数黎卡提方程(17)可以等价于下面线性矩阵不等式(26)

$\left[\begin{array}{cc}{\Pi }_{1K}^i\left(X\right)-X\left(i\right)& {\Pi }_{2K}^i\left(X\right)\\ \ast & {\Pi }_3^i\left(X\right)\end{array}\right]\le -\mu I_{n+n_v}$(26)

即有 ${\Pi }_{1K}^i\left(X\right)-X\left(i\right)\le -{\mu }_1{I}_n$，这里 $\mu >0,{\mu }_1>0$是常数，对线性矩阵不等式(26)中的1-1板块，结合式子(4)，我们可以整理得到不等式(27)如下所示：

${\displaystyle \underset{k=0}{\overset{r}{\sum }}{A}_{kK}{\left(i\right)}^T{\mathcal{E}}_i\left(X\right)A_{kK}\left(i\right)}-X\left(i\right)\le -\varsigma I_n$(27)

其中 $\varsigma >0$是常数。由文献 [18] 定理5.4可知，系统(7)的零态平衡是指数均方稳定，故闭环系统(5)是内部均方稳定的。

接下来证明 $\Vert \mathcal{T}\Vert <\gamma$。给定 $\tau \in Z_{+}$，由性能指标函数以及引理2可以得到如下等式(28)：

$\begin{array}{c}J\left(0,\tau ,v\right)={\displaystyle \underset{t=0}{\overset{\tau }{\sum }}E\left[{\Vert z\left(t\right)\Vert }^2-{\gamma }^2{\Vert v\left(t\right)\Vert }^2\right]}\\ =-E\left[x_{zs}{\left(\tau +1\right)}^{T}X\left({\eta }_{\tau +1}\right)x_{zs}\left(\tau +1\right)\right]+{\displaystyle \underset{t=0}{\overset{\tau }{\sum }}E\left[\left(\begin{array}{c}{x}_{zs}\left(t\right)\\ v\left(t\right)\end{array}\right)\left[\begin{array}{cc}{\Pi }_{1K}^{{\eta }_t}\left(X\right)-X\left(i\right)& {\Pi }_{2K}^{{\eta }_t}\left(X\right)\\ \ast & {\Pi }_3^{{\eta }_t}\left(X\right)\end{array}\right]\ast \right]}\\ =-E\left[x_{zs}{\left(\tau +1\right)}^{T}X\left({\eta }_{\tau +1}\right)x_{zs}\left(\tau +1\right)\right]+{\displaystyle \underset{t=0}{\overset{\tau }{\sum }}E\left[{\left(v\left(t\right)+{\Pi }_3^{{\eta }_t}{\left(X\right)}^{-1}{\Pi }_{2K}^{{\eta }_t}{\left(X\right)}^T{x}_{zs}\left(t\right)\right)}^T{\Pi }_3^{{\eta }_t}\left(X\right)\ast \right]}\end{array}$(28)

从上面已证明部分，可得闭环系统(5)是内部均方稳定，由文献 [12] ，当 $v\in l^2\left(0,\infty ;R^{n_v}\right)$时， $x\left(t\right)\in l^2\left(0,\infty ;R^n\right)$；故我们让 $\tau \to \infty$时，下式成立：

$\begin{array}{c}J\left(0,\infty ,v\right)={\displaystyle \underset{t=0}{\overset{\infty }{\sum }}E\left[{\left(v\left(t\right)+{\Pi }_3^i{\left(X\right)}^{-1}{\Pi }_{2K}^i{\left(X\right)}^{\text{T}}{x}_{zs}\left(t\right)\right)}^{\text{T}}{\Pi }_3^i\left(X\right)\ast \right]}\\ ={\displaystyle \underset{t=0}{\overset{\infty }{\sum }}E\left[{\left(v\left(t\right)-F\left(i\right)x_{zs}\left(t\right)\right)}^{\text{T}}{\Pi }_3^i\left(X\right)\ast \right]}\le 0\end{array}$(29)

往证 $\sup \left\{J\left(0,\infty ,v\right)<0;v\in l^2\left(0,\infty ;R^{n_v}\right),\Vert v\Vert =1\right\}<0$

利用反证法，即存在一个序列 ${\left\{v_j\right\}}_{j\ge 1}\in$使得 $\Vert v_j\Vert =1$，并且 $\underset{j\to \infty }{\lim }J\left(0,\infty ,v_j\right)=0$，则从(29)式得出：

$\underset{j\to \infty }{\lim }E\left[{\displaystyle \underset{t=0}{\overset{\infty }{\sum }}{\Vert f_j\left(t\right)\Vert }^2}\right]=0$(30)

其中 $f_j\left(t\right)=v_j\left(t\right)-F\left(i\right)x_{v_j}\left(t\right)$， $x_{v_j}\left(t\right)$是闭环系统(5)关于外部扰动输入 $v_j\left(t\right)$和初值条件 $x_j\left(0\right)=0$的解，并且关于解 $x_{v_j}\left(t\right)$相对应的闭环系统(5)可以改写成如下等式(31)：

$\begin{array}{l}{x}_{v_j}\left(t+1\right)=[\left(A_0\left({\eta }_t\right)+B_0\left({\eta }_t\right)K\left({\eta }_t\right)+M_0\left({\eta }_t\right)F\left({\eta }_t\right)\right)\begin{array}{c}\\ \end{array}\\ +{\displaystyle \underset{k=1}{\overset{r}{\sum }}\left(A_k\left({\eta }_t\right)+B_k\left({\eta }_t\right)K\left({\eta }_t\right)+M_k\left({\eta }_t\right)F\left({\eta }_t\right)\right){\omega }_k\left(t\right)}]x_{v_j}\left(t\right)\\ +\left[M_0\left({\eta }_t\right)+{\displaystyle \underset{k=1}{\overset{r}{\sum }}{M}_k\left({\eta }_t\right){\omega }_k\left(t\right)}\right]\left(v_j\left(t\right)-F\left({\eta }_t\right)x_{v_j}\left(t\right)\right)\end{array}$(31)

由于 $F\left({\eta }_t\right)$是稳定反馈增益，所以我们可以推得 $\underset{j\to \infty }{\lim }E\left[{\displaystyle \underset{t=0}{\overset{\infty }{\sum }}{\Vert x_{v_j}\left(t\right)\Vert }^2}\right]=0$，与此同时有： $\underset{j\to \infty }{\lim }E\left[{\Vert v_j\left(t\right)\Vert }^2\right]\le 2\underset{j\to \infty }{\lim }E\left[{\Vert f_{{\eta }_t}\left(t\right)\Vert }^2\right]+2\underset{j\to \infty }{\lim }E\left[\Vert F\left({\eta }_t\right)x_{v_j}\left(t\right)\Vert \right]=0$

显然，上式与 $\Vert v_j\Vert =1$矛盾。因此 $J\left(0,\infty ,v\right)<0$，即 ${\Vert \mathcal{T}\Vert }_{\infty }<\gamma$，故1)成立。

最后来证明2) $\Rightarrow$3)：

已知代数黎卡提方程(17)的稳定解为 $X\in {\mathrm{H}}_{\infty }^{n+}$，运用舒尔补技巧，我们可以得到对所有的 $i\in S$，代数黎卡提方程(17)等价于下面线性矩阵不等式LMI

$\left[\begin{array}{cccc}-X& 0& {\Phi }_1^i\left(X\right)& C{\left(i\right)}^T+K{\left(i\right)}^{T}D{\left(i\right)}^T\\ \ast & -{\gamma }^{2}I& {\Phi }_2^i\left(X\right)& G{\left(i\right)}^T\\ \ast & \ast & -\mathcal{X}& 0\\ \ast & \ast & \ast & -I\end{array}\right]<0$(32)

其中

${\Phi }_1^i\left(X\right)=\left[\left(A_0{\left(i\right)}^T+K{\left(i\right)}^T{B}_0{\left(i\right)}^T\right)X,\cdots ,\left(A_r{\left(i\right)}^T+K{\left(i\right)}^T{B}_r{\left(i\right)}^T\right)X\right]$

${\Phi }_2^i\left(X\right)=\left[M_0{\left(i\right)}^{T}X,\cdots ,M_r{\left(i\right)}^{T}X\right]$

$\mathcal{X}=diag\underset{r+1}{\underset{︸}{\left\{X,X,\cdots ,X\right\}}}$

对上面线性矩阵不等式(32)左乘和右乘 $diag\left\{X^{-1},I,{\mathcal{X}}^{-1},I\right\}$得到如下不等式

$\left[\begin{array}{cccc}-X^{-1}& 0& X^{-1}{\Phi }_1^i\left(X\right){\mathcal{X}}^{-1}& X^{-1}\left(C{\left(i\right)}^T+K{\left(i\right)}^{T}D{\left(i\right)}^T\right)\\ \ast & -{\gamma }^{2}I& {\Phi }_2^i\left(X\right){\mathcal{X}}^{-1}& G{\left(i\right)}^T\\ \ast & \ast & -{\mathcal{X}}^{-1}& 0\\ \ast & \ast & \ast & -I\end{array}\right]<0$(33)

其中令 $Y=X^{-1},K\left(i\right)=W\left(i\right)Y^{-1}$，则对所有的 $i\in S$，从上面线性矩阵不等式(33)可以推得以下不等式

$\left[\begin{array}{cccccc}-Y& 0& {\Phi }_0& \cdots & {\Phi }_r& \Xi \\ \ast & -{\gamma }^{2}I& M_0^{\text{T}}\left(i\right)& \cdots & M_r^{\text{T}}\left(i\right)& G^{\text{T}}\left(i\right)\\ \ast & \ast & -Y& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \ast & \ast & \ast & \cdots & -Y& 0\\ \ast & \ast & \ast & \cdots & \ast & -I\end{array}\right]<0$(34)

对于上面不等式中的 $-{\gamma }^{2}I$板块，利用舒尔补定理，我们可以得到上式等价于下面线性矩阵不等式(35)：

$\left[\begin{array}{cccccc}-Y& {\Phi }_0& {\Phi }_1& \cdots & {\Phi }_r& \Xi \\ \ast & {{\rm T}}_{00}-Y& {{\rm T}}_{01}& \cdots & {{\rm T}}_{0r}& {\gamma }^{-2}{M}_0\left(i\right)G{\left(i\right)}^T\\ \ast & \ast & {{\rm T}}_{11}-Y& \cdots & {{\rm T}}_{1r}& {\gamma }^{-2}{M}_1\left(i\right)G{\left(i\right)}^T\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \ast & \ast & \ast & \cdots & {{\rm T}}_{rr}-Y& {\gamma }^{-2}{M}_r\left(i\right)G{\left(i\right)}^T\\ \ast & \ast & \ast & \cdots & \ast & {\gamma }^{-2}G\left(i\right)G{\left(i\right)}^T-I_{n_z}\end{array}\right]<0$(35)

不等式(35)左、右乘 $diag\underset{r+3}{\underset{︸}{\left\{\gamma I,\gamma I,\cdots ,\gamma I\right\}}}$，并且让 ${\gamma }^{2}Y$作为新的变量，则对所有的 $i\in S$，线性矩阵不等式(35)可以等价为线性矩阵不等式(18)。

故2) $\iff$3)证毕

综上所述定理1得以证明。

4. 结束语

近几年，关于随机系统有界实引理的研究被广泛应用于H_∞控制问题中。本定理考虑的是在离散时间无限马尔可夫无限时域H_∞控制问题，利用舒尔补技巧得到线性矩阵不等式、黎卡提方程稳定解的等价性、系统内部均方稳定性之间的等价性，即H_∞控制问题和系统内部均方稳定性之间的等价性，为控制器的设计提供了新的方法。

基金项目

重庆理工大学研究生教育高质量发展行动计划资质成果，项目编号：gzlcx20223304，项目类型：校级联合资助项目。