1. 引言
负荷预测是保证电力供需平衡的基础 [1] 。目前我国的负荷预测方法已经呈现多样化 [2] ,其中一种常用方法是根据电力负荷历史数据来推测未来数值,充满了不确定性 [3] [4] 。这种基于历史数据的负荷预测最主要的问题就是解决预测模型的精度问题,如何消除预测模型里的不确定因素,尽可能精确地预测电力负荷的大小。
近些年来,随着科学技术的迅速发展,预测的方法与理论知识不可同日而语,随着人工智能的普及,新的预测方法层出不穷,为电力负荷预测研究提供了有力的工具。具体来说,中国电力企业已经采用了各种预测方法和技术,包括时间序列分析 [5] 、神经网络 [6] 、支持向量机 [7] 、遗传算法 [8] 等。这些方法和技术能够有效地预测不同地区的负荷需求,提高电力调配的准确性和效率。此外,中国电力企业还积极推广智能电网技术 [9] [10] ,通过实时监测和分析用电数据,预测未来用电趋势,并根据预测结果进行电力调配,从而提高电力供给的质量和稳定性。总的来说,中国电力企业在区域负荷预测方面已经取得了显著的进展,不断引入新的技术和方法,以适应电力市场和用电需求的不断变化。
在此基础上,本文将重点放在LSTM以及ARIMA两种方法上,将ARIMA作为对照组,LSTM作为实验组,对比两种预测方法的优缺点。
2. 原理
2.1. 数据预处理
对收集到的数据进行归一化的预处理,可以防止数据输入到LSTM中导致网络神经元饱和,影响预测网络的准确性。其归一化表达式为:
(1)
式中Y表示原始数据归一化后的数据;X表示原始输入数据;
表示原始数据中的最小值;
表示表示原始数据中的最大值。
2.2. LSTM神经网络的模型原理
LSTM是一种基于时间序列的长短期记忆网络。LSTM神经网络中能够通过更新或移除来实现选择通过信息的节点称为“门”结构,神经网络中包含三种门结构:输入门,输出门,遗忘门。输入门决定哪些信息可以进入细胞,遗忘门决定每一时刻是否有信息被遗忘,而输出门则决定哪些信息是有效的并被输出。其基本的结构原理图见图1:
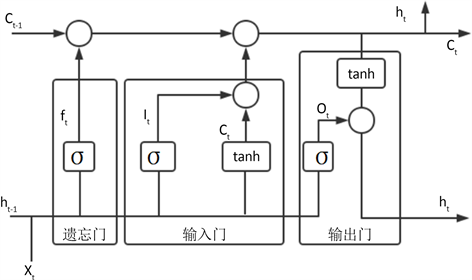
Figure 1. Schematic diagram of LSTM model
图1. LSTM模型原理图
前一个记忆单元
由遗忘门
控制保留至当前记忆单元
的信息量;输入
由输入门
决定保留至当前记忆单元
的信息量;当前记忆单元
由输出门
控制输出到
的信息量。LSTM的公式如下:
记忆单元:
遗忘门:
输入门:
(2)
输出门:
最终输出:
2.3. ARIMA预测原理
ARIMA (Autoregressive Integrate Moving Average)是一种广泛应用于时间序列分析中的统计模型,用于预测未来的趋势和波动。ARIMA模型基于对时间序列数据的分析,包括分析趋势、季节性和随机性等特征,以及进行差分和平滑处理,以便将时间序列转化为平稳的序列。ARIMA模型在电力预测中应用广泛,可以用于预测电力负荷、电价、电量等指标。
ARIMA模型由三个参数来描述时间序列,分别是p、d、q,其中:
p表示自回归(AR)项,表示当前时刻的值与之前p个时刻的值之间的关系;
d表示差分(I)项,表示需要进行几次差分才能使序列平稳;
q表示移动平均(MA)项,表示当前时刻的值与之前q个时刻的噪声项之间的关系。
3. 负荷预测过程
3.1. LSTM预测流程
预测需要多方面验证LSTM模型预测的准确性,故采用多组对照实验。将不同时间尺度实验组的预测结果,以及同一时间尺度下用LSTM方法、ARIMA两种方法进行预测的结果分别进行对照分析。预测步骤如下:
1) 导入某地区某年的区域负荷数据样本数据集,对样本数据集进行预处理。预处理包括归一化处理和划分训练集。根据不同的时间分度,将每组数据按6:2:2划分训练集、测试集和验证集;
2) 搭建LSTM神经网络模型。设置神经元核心的个数,迭代次数,优化器等。输入训练集训练LSTM网络,通过对比分析预测结果,调整模型参数;
3) 向训练好的LSTM神经网络输入测试集,预测下一个时间段的用电负荷,以此类推,实现滚动预测。选取合适的评价指标的预测结果进行分析。
3.2. ARIMA预测流程
ARIMA模型的搭建过程通常可以分为以下几个步骤:
1) 数据准备:收集并准备好时间序列数据,确保数据完整、连续、准确。
2) 数据预处理:对原始数据进行必要的预处理,如填充缺失值、一阶差分和二阶差分等。
3) 确定ARIMA模型阶数:通过分析时间序列数据的未平稳与一阶差分后的自相关函数ACF和偏自相关函数PACF,并根据AIC、BIC准则,以及对残差序列的分析,选择合适的ARIMA模型阶数。
4) 模型训练:使用选定的ARIMA模型阶数,对数据进行训练。
5) 模型检验:对训练出来的模型进行检验,包括检查残差序列的正态性和自相关性等,以确保模型具有良好的性质和可靠性。
6) 模型预测:使用训练好的ARIMA模型进行预测,可以预测未来某一时刻或一段时间内的数据。
7) 模型评估:对模型预测结果进行评估,比较预测值与实际值之间的误差,根据MAE、RMSE两个评价指标对模型进行优化和改进。
3.3. 评估指标
为了评估模型性能,本文采用平均绝对误差(MAE),均方根误差(RMSE)。数学表达式如式(3)~(4)所示。
(3)
(4)
4. 负荷预测案例分析
4.1. 数据集处理
本文收集的是A地区2016年一年的用电负荷量,采样间隔为15分钟,共35,316个数据。在归一化处理后,根据不同的时间尺度,分为三组,分别选取一年、一个月、一天的数据,划分前60%的数据为训练集,中间20%的数据为测试集,末尾20%的数据为验证集。
4.2. LSTM模型搭建过程
4.2.1. 训练模型
初始隐态向量设置为16,LSTM单元分别设置为32和64,每次使用16个自变量来预测1个因变量,输出维度为设置为2,迭代次数设置为100,dropout参数为0.1、patience参数为20。设定后将训练集放入LSTM中进行训练,并加入验证集进行验证,得出符合数据特点的模型。
4.2.2. 停止训练的条件
停止训练有两种情况:训练过程中达到epoch最大值或满足符合提前停止的次数上限时,该训练则停止,模型训练完成。
4.2.3. 参数设置
参数设置见表1。

Table 1. LSTM model parameter settings
表1. LSTM模型参数设置
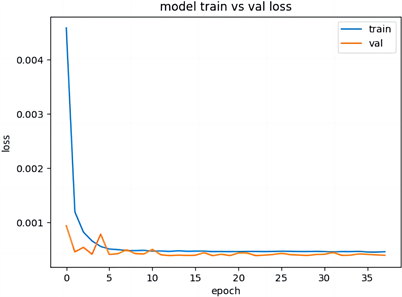
Figure 2. Annual forecast loss graph
图2. 年预测的损失曲线图
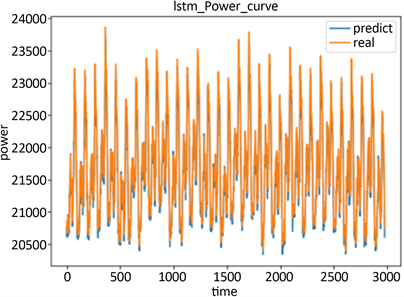
Figure 3. The annual predicted value versus the true value (MW)
图3. 年预测值和真实值对比图(MW)
4.3. 结果分析
年预测组的训练集和验证集损失曲线见图2,预测值和真实值对比图见图3。
月预测组的最终训练损失曲线见图4,真实值与预测值对比图见图5。
日预测组的最终训练损失曲线见图6,绘制真实值与拟合值对比图见图7。
电力负荷预测是具有高度随机性和变化性的数据,比较上图可得,LSTM模型在这三组不同时间尺度的预测中,预测值和真实值的曲线接近,预测效果良好,三组训练集和预测集的曲线相关性均较强,验证了LSTM预测方法的准确性。所收集负荷数据平均值为20,635.11 MW,由评估指标MAE和RMSE可以得出真实值和预测值偏离的相对误差均在3%以下,可以用于本案例负荷预测。其中年预测和月预测的准确性更高,可见LSTM更适合长期预测。
三组预测模型的测试的准确性见表2:
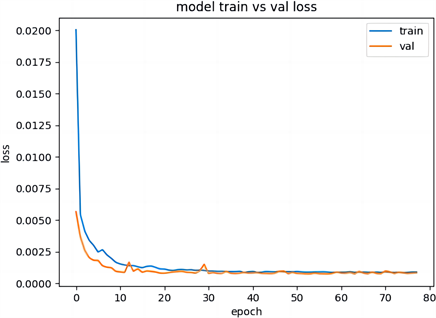
Figure 4. Monthly forecast loss graph
图4. 月预测的损失曲线图
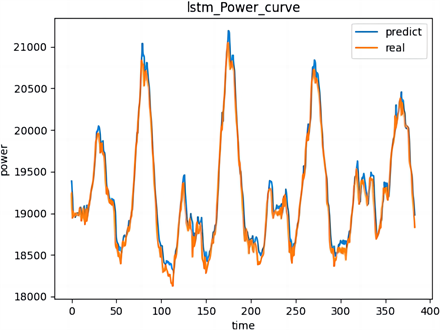
Figure 5. Graph of the predicted and true monthly values (MW)
图5. 月预测值和真实值对比图(MW)

Figure 7. Daily predicted value versus true value (MW)
图7. 日预测值和真实值对比图(MW)

Table 2. Prediction evaluation index (MW)
表2. 预测评估指标(MW)
4.4. ARIMA模型搭建过程
4.4.1. 数据预处理
对原始数据进行填充缺失值处理,采用n = 2的n最近邻均值法填充,并对填充缺失值后的数据进行一阶差分与二阶差分。
4.4.2. 确定ARIMA模型阶数
通过分析时间序列数据的未平稳与一阶差分后的自相关函数ACF和偏自相关函数PACF,并结合AIC、BIC准则,确定ARIMA模型的p、q参数,p = 4、q = 0。对原数据与一阶差分后的数据进行ADF检验,得到p < 0.05小于显著性水平,我们即可认为序列具有平稳性,则确定ARIMA模型的d = 1。即(p,d,q) = (4,1,0)。划分训练集、测试集和验证集同LSTM模型。
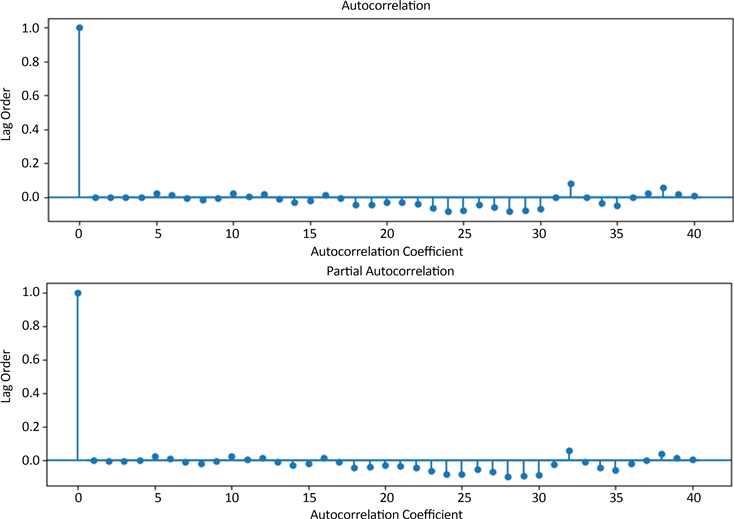
Figure 8. Residual ACF and PACF plots
图8. 残差ACF与PACF图

Figure 9. Residual normality test QQ graph
图9. 残差正态性检验QQ图
4.4.3. 模型检验
在ARIMA负荷预测中,进行了多种检验,有效地对模型进行评估和选择,提高预测的准确性和可靠性。其中,pvalue = 4.07974,DW检验结果为2.00187。残差ACF与PACF图见图8,残差正态性检验QQ图见图9,残差正态性检验直方图见图10。这些检验从不同角度评估了模型的合适性,确保了模型的稳定性、可靠性和准确性。
4.4.4. 模型预测
原数据与预测数据对比图见图11:
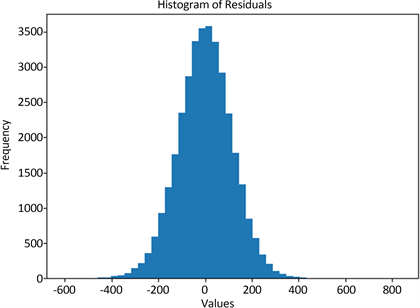
Figure 10. Histogram of residual normality test
图10. 残差正态性检验直方图
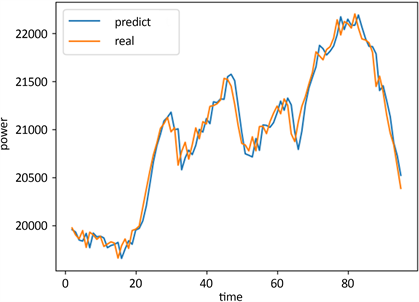
Figure 11. Graph comparing original data with predicted data (MW)
图11. 原数据与预测数据对比图(MW)
从原数据与预测数据对比图看出ARIMA模型拟合效果较好,但有些值偏高或偏低。
4.4.5. 模型评估
RMSE (Root Mean Squared Error):均方根误差,是MSE的平方根。RMSE越小,说明预测结果越准确。
MAE (Mean Absolute Error):平均绝对误差,是预测值与实际值之差的绝对值的平均值。MAE越小,说明预测结果越准确。
最终由ARIMA模型拟合出的均方根误差RMSE = 1117.10 MW,平均绝对误差MAE = 890.12 MW。LSTM模型的MAE为95.18 MW,RMSE为120.68 MW,而ARIMA模型的MAE为890.12 MW,RMSE为1117.10 MW,说明LSTM模型在预测误差方面表现更优秀。因此,在实际应用中,可以优先考虑使用LSTM模型进行电力负荷预测,同时也需要根据实际情况进行选择和调整。
5. 结语
本文基于LSTM和ARIMA模型,形成了相应预测流程,根据区域负荷历史数据进行预测。区域负荷预测案例分析结果表明,在均方根误差和平均绝对误差两项指标中,LSTM通常比ARIMA的预测更精确,但ARIMA模型具有更强的可解释性,只需要进行参数估计和预测就能够清楚地展示趋势和周期性,LSTM模型的预测结果则需要进一步解释其内部神经网络结构的作用且LSTM的计算复杂度更高,需要大量计算资源和时间。综合来说,应根据具体应用场景选择合适的模型:对于简单的平稳时间序列数据,ARIMA更适合;对于复杂的非线性时间序列数据,LSTM更具优势。
基金项目
中央高校基本科研业务费专项资金;中国矿业大学(北京)大学生创新训练项目(202204020)。