1. 引言
第五代移动通信技术(5G)在2020年之后已经逐渐商用,其通信网络也已在全球范围内大规模部署 [1] 。随着经济社会向数字化、网络化、智能化转型,诞生了一大批以智慧城市、智慧交通、智能家居为代表的B5G/6G时代的新兴应用场景。但是这些新兴业务对移动通信网络端到端的信息处理能力提出了更高的要求,其处理流程一般呈现出通信感知高度融合的特点:
· 通信环节和感知环节在时空域交叠。
· 通信功能与感知功能相互影响。
· 感知能力和通信能力具有一致的大带宽频谱和大孔径天线的需求。
这些特点促进了现有无线网络架构和相关技术向资源高效利用、差异化应用智能适配的新型网络结构和使能技术转型,催生了通信感知一体化(Integrated Sensing and Communication, ISAC)网络架构与相关技术的研究和发展 [2] 。通信感知一体化技术的核心理念是要让无线通信和无线感知两个独立的功能在同一系统中实现且相互增强,例如基站通过分析无线信号的直射、散射或反射信号对周围环境的属性和状态进行感知 [3] ,设计传输信号的预编码矩阵,更好地消除环境干扰。
位置信息的感知获取是通信感知一体化的关键技术之一。微型无线网设备和无人机数量的激增使得城市信号源的密度提升,借助密集部署的宏小区和小小区,基站在超密集环境中的覆盖无处不在 [4] ,这为位置感知技术的应用提供了便利的条件。在密集网络中提供位置信息的位置模块可以放置在基站处,从而向导航工具提供从网络端发送位置信息的选择,而不再依赖全球定位系统 [5] 。同时,5G网络还可以通过感知获得的用户位置信息和环境地图提高密集城市网络中的通信吞吐量 [6] 。针对5G网络内物体的有效位置信息中方向信息的获取,目前有专家利用5G毫米波(Millimeter Wave, mmWave)信道的稀疏特性估计信号角度 [7] [8] ,有的利用5G新空口(New Radio, NR)系统中特殊的导频序列对方向角进行估计 [9] [10] 。本文则根据窄带信号的多径角估计算法,提出了适用于5G网络OFDM系统的多径角估计算法,利用下行同步中主同步序列良好的自相关特性实现对5G基站方向角的估计。
本文后续章节安排如下:章节2介绍5G通信系统中的下行同步过程;章节3介绍多径角估计算法的理论模型及仿真结果,章节4介绍基于多径角估计算法的5G基站测向算法,章节5总结全文的主要成果。
2. 5G系统的下行同步过程
5G物理层作为5G通信系统的能力核心,对来自媒质访问控制(Medium Access Control, MAC)层的数据进行处理并提供物理传输通道 [11] ,其中下行同步信号通过物理广播信道(Physical Boardcast Channel, PBCH)进行传输。终端在开机后首先通过检测基站定期发送的同步信息块(Synchronization Signaling Block, SSB)中的同步信号(Synchronization Signal, SS)和物理广播信道数据(PBCH Data)实现下行同步(包括频率同步和时间同步),获取小区ID、中心频率、带宽和帧结构等基本信息,进而根据下行同步过程接收的系统信息发起随机接入过程。
一个SS/PBCH块的结构如图1所示,是由主同步信号(Primary Synchronization Signal, PSS)、辅同步信号(Secondary Synchronization Signal, SSS)、物理广播信道以及解调参考信号(Demodulation Reference Signal, DMRS)四部分组成。SS/PBCH中梳状插入DMRS,DMRS的起始位置由物理小区标识
模4确定,以实现小区间的正交 [12] 。终端在进行下行同步时首先要进行小区搜索,对可能的3条主同步信号进行盲检测,得到相应的主同步信号,并获取物理小区标识2的值(
),接着对可能的336条辅同步信号进行盲检测,获取物理小区标识1的值(
)。通过上述过程获取的两个物理小区标识,终端计算出物理小区ID号为
。在对同步信号进行检测的过程中,利用同步信号的相关性,可以同时实现下行时间同步和频率同步。在完成这些步骤后,进行DMRS信号的解调,接收PBCH中的主消息块(Master Information Block, MIB),获得系统帧号(System Frame Number, SFN)和半帧指示,从而完成无线帧定时以及半帧定时,下行同步完成。

Figure 1. Schematic diagram of SSB structure
图1. SSB结构示意图
3. 多径角估计算法及其仿真结果
无线网络中的信号在传播过程中会遇到各种障碍物,从而发生散射、衍射、折射和绕射。这会导致同一信号经过不同的时延到达接收机,在时延域上产生多径现象。在实际的5G通信系统中,接收机所接受的信号是同一信号的不同路径以及不同信号的叠加,分析信号来波方向困难重重。目前常用的方法是通过对接收信号进行解相干处理,利用子空间的估计方法估计信号来波方向 [13] 。但这种方法处理的接收信号经过解相干后,各个信号被视为独立的信号,不能分辨信号的多径,因此有人提出了使用伪随机序列(PN)的阵列响应(MAPS)测量和估计传播路径二维DoA的方案 [14] 。该方案假设发送信号是窄带信号,通过使用接收平面天线阵列(PAA),MAPS首先为每个传播路径提取复杂路径阵列响应向量(PARV),然后单独且独立地估计路径的DoA。该方法不仅避免了相干信号的干扰,而且还能分辨出信号的多径。本文基于该算法的数学原理,将其从窄带信号推广至5G网络的OFDM系统中,完成对5G基站的测向感知仿真。
3.1. 系统模型
如图2所示,考虑一个OFDM移动通信系统模型。在该系统中,有多个基站和若干个用户,基站和用户都配备单天线。此外,接收机配备沿yz平面放置的
的均匀平面天线阵,
表示沿z轴方向摆放的天线数,
表示沿y轴方向摆放的天线数。记
,K表示天线阵元的总个数,天线间距
,
是接收阵列所接收到最大频率信号所对应的波长。
发送信号时域表示如下式所示:
(1)
其中,
是一个持续时间为
的矩形窄脉冲,N表示发送时域序列的长度,
是矩形窄脉冲幅度。
符号速率为
。
空间时域信道脉冲响应模型表示如下式所示:
(2)
其中,L是多径的数量;
表示第l条路径的信道增益;
表示第l条路径对信号的相位影响;
表示第l条路径的时延;
、
是第l条路径的方位角和仰角;
是频率为f的信号在第l条路径的转向矢量,它可以表示成如下形式:
(3)
由几何关系,可以得到:
(4)
(5)
(6)
由于天线的工作频率是3.5 GHz,而载波间隔是15 KHz,考虑到仿真所使用的频域序列长度 ≤ 240,信号的中心频率远大于信号带宽,所以
(7)
因此,我们有
(8)
(9)
(10)
(11)
前面我们给出了发送信号时域表达以及信道脉冲响应的时域表达,那么接收信号等于发送信号与信道脉冲响应的卷积,具体表达式如下式所示:
(12)
其中,m表示第m个天线阵元,
表示发送信号
经过时延
到达天线阵的信号;
是第m个天线阵元的复转向因子;令
,表示第l条路径的复增益;
表示信道噪声,它服从高斯分布。
3.2. 多径角估计算法
对接收信号和发送信号做自相关,可以得到:
(13)
其中,
表示发送符号的平均能量,并且有:
(14)
(15)
由于发送序列具有良好的自相关性,所以会在时延域不同的时延上形成L个峰值,如图3所示:
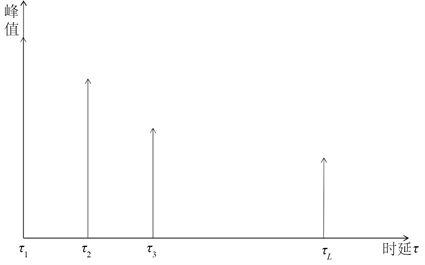
Figure 3. The time delay domain peak of the mth array element
图3. 第m个阵元的时延域峰值
上文提到,第m个阵元会在时延域不同的时延上形成L个峰值,峰值的强度是
。我们将第m个阵元的峰值合并起来,得到一个行向量,记为:
(16)
那么接收天线阵列所输出的所有峰值可以表示成如下形式:
(17)
其中,第M行表示第M个阵元的输出,第l列表示包含第l条路径所有的峰值。我们把A的列称为是第l条路径的路径响应矢量,它对应于一条独立的路径。
第l条路径的路径响应矢量进一步表示为:
(18)
其中,
是K维矢量,它指向第l条路径的DoA。我们的目标是根据观察到的路径响应矢量确定
。
的
维协方差矩阵可以计算为(为了便于表述,我们忽略了
):
(19)
容易得到,
的秩是1,并且它的特征值满足:
(20)
那么
的特征值
对应的特征向量
便是指向第l条路径的特征矢量。因此,我们有如下引理:
正交于其他零特征值所对应特征向量构成的空间,即:
(21)
其中,
的空间被称为参考子空间,因此我们可以得出所有指向第l条路经的转向矢量
都正交于参考子空间。因此,空间频谱可以如下定义:
(22)
空间频谱谱峰对应的角度即为我们所求的目标方向角。
3.3. 仿真结果
为了测试多径角估计算法的感知性能,我们采用序列长度为720、根索引为650的Zadoff-Chu (ZC)序列作为发送信号,采用2 × 4的平面天线阵列作为接收天线,利用QuaDRiGa信道为发射机–接收机信道生成信道系数和信道时延。QuaDRiGa信道仿真参数配置如表1所示:

Table 1. Simulation parameters of QuaDRiGa channel
表1. QuaDRiGa信道的仿真参数
利用QuaDRiGa信道生成的接收机和发射机相对位置如图4所示:红色正三角图标表示接收机周围的散射体簇的中心位置,黄蓝色小圆圈图标表示发射机的位置,黄红色小方块图标表示接收机的位置。由图4,我们可以得到发射机、接收机以及接收机周围散射体的物理位置,具体数值见表2。

Figure 4. Relative position of receiver and transmitters
图4. 接收机和发射机的相对位置

Table 2. Physical coordinates of transmitters and scatterers (unit: m)
表2. 发射机和散射体的物理坐标(单位:m)
我们根据发射机和散射体相对于接收机的位置关系计算发射机和散射体的角度,接着利用QuaDRiGa信道在不同信噪比(SNR,单位:dB)进行算法仿真验证,仰角测量值和理论值见表3,方位角的测量值和理论值见表4。

Table 3. Elevation measurement results at different signal-to-noise ratios and theoretical values of elevation angle
表3. 在不同信噪比下的仰角测量结果以及仰角理论值

Table 4. Azimuth measurement results at different signal-to-noise ratios and theoretical values of azimuth
表4. 在不同信噪比下的方位角测量结果以及方位角理论值
我们用
来衡量多径角估计算法的性能,其中,
是方位角理论值与估计值的差值,
是仰角估计值与理论值的差值,在不同信噪比下多径角估计算法的性能如图5所示。仿真结果表明,发射机的方向角测量结果误差很小,而散射体的方向角测量结果误差较大,而且随着信噪比的增加,无论是散射体还是发射机的误差都在减小。同时,在不同信噪比下散射体的方位角测量值和仰角测量值差别不大,这说明噪声对散射体方位角和仰角误差的影响较小。再进一步观察,我们发现随着信噪比的增加,散射体方向角和仰角都在趋近于一个值。当然,这个值不是理论值。这说明由于散射体的物理位置不准确从而导致了散射体方位角和仰角的误差较大。在无线信道环境中,散射体通常用簇来表示。一簇散射体其他若干微小物体组成。为了方便计算散射体方位角和仰角,本文利用散射体的几何中心的物理位置来表示散射体的物理位置,从而导致一定的系统误差。但在误差允许的范围内,多径角估计算法可以正确地分辨信号多径。
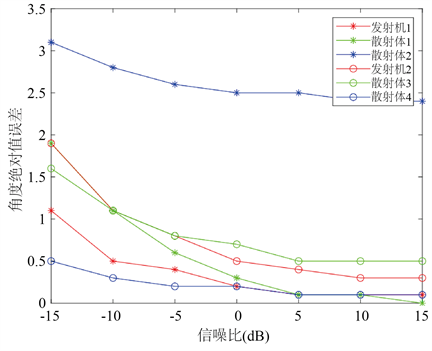
Figure 5. Performance of multipath angle estimation algorithms with different signal-to-noise ratios
图5. 不同信噪比下多径角估计算法性能
4. 5G基站测向设计
4.1. 测向流程
在5G通信系统的下行同步过程中,图1所示的SSB内的PSS序列具有很好的自相关特性,因此我们使用它作为5G基站测向的依据。PSS序列是三条长度为127的m序列。m序列又称为最长线性反馈移位寄存器序列,由初始序列经过循环移位得到,其中初始序列是由本原多项式的系数得到。PSS序列具体生成公式如下:
(23)
(24)
(25)
其中,
,
,并且m序列初始寄存器的情况为
。
基站方向感知算法要求接收机接收到SSB后检测PSS序列并利用多径角估计算法估计基站到达接收机路径的角度。具体步骤与仿真流程如下:
i) 生成包含SS burst、MIB和SIB1的波形,配置物理小区标识,模拟5G通信系统无线信号,具体参数见表5。
ii) 发送波形通过QuaDRiGa信道生成接收波形。由于QuaDRiGa信道不生成噪声,所以需要设置信噪比并向接收波形添加高斯白噪声。
iii) 在不同频率点上利用所有可能的PSS序列与接收波形作互相关,得到频偏和物理小区标识2。
iv) 利用频偏和物理小区标识2对应的互相关峰值结果,用多径角估计算法估计基站和散射体到达接收机路径的角度。

Table 5. Base station direction-aware simulation parameters configuration
表5. 基站方向感知仿真参数配置
4.2. 基站方向感知仿真结果
在仿真中接收机采用沿yz平面放置2 × 4的平面天线阵列作为接收天线,利用QuaDRiGa信道为发射机–接收机信道生成信道系数和信道时延。QuaDRiGa信道具体仿真参数配置见表1。QuaDRiGa信道生成的基站、散射体与接收机的相对位置见图6。红色正三角图标表示接收机周围的散射体簇的中心位置,黄蓝色小圆圈图标表示基站的位置,黄红色小方块图标表示接收机的位置。由图6,我们可以得到基站、接收机以及它们周围散射体的物理位置,具体数值见表6。

Table 6. Physical coordinates of base stations and scatterers (unit: m)
表6. 基站以及散射体的物理坐标(单位:m)

Figure 6. Physical location of base stations, scatterers and receiver
图6. 基站、散射体与接收机的物理位置
我们根据基站和散射体与接收机的相对位置计算出基站和散射体的角度,接着利用QuaDRiGa信道在不同信噪比下测量基站和散射体相对于接收机的仰角和方位角。仰角测量值和理论值见表7,方位角的测量值和理论值见表8。

Table 7. Elevation measurement results at different signal-to-noise ratios and theoretical values of elevation angle
表7. 在不同信噪比下的仰角测量结果和仰角理论值

Table 8. Azimuth measurement results at different signal-to-noise ratios and theoretical values of azimuth
表8. 在不同信噪比下的方位角测量结果和方位角理论值
我们同样使用
来估计基站测向误差,并绘制误差曲线图。在不同信噪比下的基站和散射体方向角误差见图7。
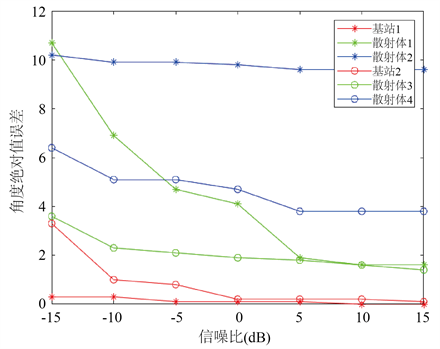
Figure 7. Base stations and scatterers orientation angle error
图7. 基站和散射体方向角误差
从图7可以得到:基站的方向角测量结果误差很小,而散射体的方向角测量结果误差较大,这主要是由于我们用散射体中心的物理位置来表示一簇散射体的物理位置而产生的系统误差。而且随着信噪比的增加,无论是散射体还是基站的方向角误差都在下降。
为了更加直观地显示基站和散射体相对于接收机的方向,图8和图9仿照波束方向图给出了在0 dB情况下的基站和散射体的方向图,来反映基站、散射体相对于接收机的位置。在方向图中用颜色表示信号能量,横坐标为仰角的正弦函数,纵坐标是方位角的正弦与仰角的余弦之积。颜色越亮,表示信号能量越强。图8和图9均有三处颜色较亮区域,这些区域清晰地表示了基站和散射体相对于接收机的方向。
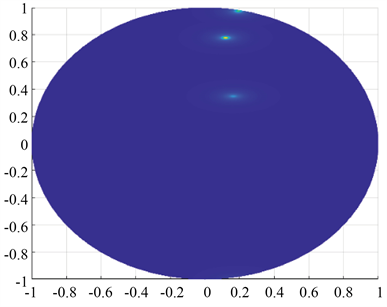
Figure 8. Directional diagram of base station 1 and surrounding scatterers at 0 dB
图8. 0 dB情况下基站1及周围散射体的方向图

Figure 9. Directional diagram of base station 2 and surrounding scatterers at 0 dB
图9. 0 dB情况下基站2及周围散射体的方向图
5. 结束语
本文围绕5G移动通信系统信号源的测向展开研究,将多径角估计算法推广到OFDM系统中,提出了一种基于下行同步过程中PSS序列感知5G基站方向角的算法,并利用准确定性无线信道产生器在不同信噪比下对算法性能进行仿真。该算法可以在误差允许的范围内感知基站和散射体相对于接收机的方位角,从而能直观地显示基站和散射体相对于接收机的方向。该算法可以应用在智能反射面上,对接收信号的路径进行角度估计,使其具有感知测量能力,对未来通信感知一体化技术的发展具有重要意义。