1. 引言
页岩气作为重要的能源资源,对于国家工业、经济社会等的发展具有重要影响和战略意义。目前,水平井分段压裂是页岩储层成功改造的关键技术,国内外学者针对压裂后的页岩储层建立了大量的数学模型,描述页岩气的多重输运物理机制,分析页岩储层压裂后的产气规律等 [1] [2] 。然而,多数页岩气井都具有较长的产水期,但大部分数学模型忽略了返排阶段压裂液对产气规律的影响,造成产气量预测结果偏大。不仅如此,压裂后的页岩储层包含天然裂缝和人工裂缝以及基质孔隙,介质类型复杂,孔缝尺度跨越几个量级。因此,裂缝型多孔介质的多相渗流模型是一项非常具有挑战性的课题,对于理解渗流机理和压裂后产气量预测具有重要的理论和实践价值。
实验方法可以直接获得裂缝型多孔介质多相渗流的相对渗透率,但一般需要较长的时间和较高的成本,且对于一些低渗多孔介质往往很难直接测得相对渗透率,测量结果缺乏普适性 [3] 。随着计算机技术的发展,数值模拟方法也被应用到多孔介质气液多相渗流的研究中,但得出的结论通常含有经验参数,物理机理不清晰 [4] 。基于欧氏几何的传统分析方法一般仅适用于简单结构,很难构建实用的、符合客观规律的多孔介质多相渗流解析模型 [5] 。大量研究表明,多孔介质的裂缝网络、固相质量、孔隙面积、弯曲流道等均表现出统计自相似分形标度行为,分形几何为表征多孔介质的复杂微细结构提供了一种有效的数学工具和方法 [6] [7] [8] 。虽然多个学者提出不同的分形模型用以研究多孔介质气液两相渗流特性,但大多分形模型忽略了裂缝之间的交叉连通特征,而页岩储层中的压裂裂缝显示出分形分叉网络拓扑结构,扮演着页岩气的主要运移路径 [9] 。因此,本文采用分形分叉网络来定量表征裂缝型页岩储层的裂缝网络结构,其中分叉网络拓扑结构利用最小化流阻原理 [10] 进行结构优化,并将分形分叉网络嵌入各向同性均质多孔基质发展一种分形双重介质模型,推导裂缝型多孔介质气液两相渗流的相对渗透率,并采用有限元方法构建裂缝型多孔介质气液两相渗流的数学模型,研究裂缝网络中的局域流动特性和规律。
2. 气液两相渗流的分形双重介质模型
2.1. 裂缝网络渗流模型
考虑如图1所示的立方体代表性单元(REV),采用分形分叉网络模型表征裂缝拓扑结构。假设分形分叉网络的数目具有统计自相似分形标度律 [11] :
(1)
式中,
表示0级母管的最大半径,N是0级母管半径大于
的数目,
是裂缝母管半径分形维数,其范围是
。假设方程(1)是连续的和可微的,0级母管孔径从
到
的数目可以表示为:
(2)
因此,到第0级裂缝母管半径
的概率密度函数为:
(3)
裂缝母管半径分形维数
与孔隙率
之间存在如下标度关系 [11] :
(4)
式中下标min和max分别表示最小和最大孔径,
为欧氏维数,此处
。由于分形概率密度函数需满足归一化条件,因此裂缝网络0级母管的尺度满足
。实践中,通常将
作为满足分形标度律的条件。由此可得裂缝母管横截面积为:
(5)
则垂直于流动方向的横截面积可以表示为
。
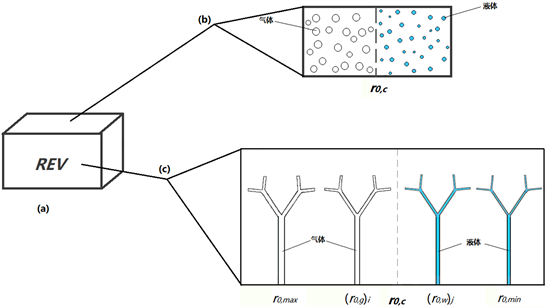
Figure 1. Diagram of a fractal dual-medium model for fractured porous media
图1. 裂缝型多孔介质分形双重介质模型示意图
典型的分形分叉网络可以通过迭代算法生成。通常单根分叉网络是由一母管按照一定的分叉角度分叉出两个或多个子管,然后每个子管按照相同的规则分叉出更多的分叉管道,不断重复这一分叉过程形成的,假设分叉网络的母管长度
相同,且每一级分叉管道均是圆形直管且管壁厚度可以忽略不计。图2所示的是一个典型的双分叉分形网络。对于其中任意一级分叉而言,分别用
和
表示第k (
)级分叉管道的直径和长度,
和
表示第
级分叉管道的直径和长度,分叉角为
,最大分叉级数为m,分叉数为
(图2中
)。引入两个描述分叉网络几何结构的尺度因子来表示相邻两级分叉的长度比和直径比:
(6)
(7)
由于网络具有分形特征,要求分叉数和分叉比保持常数(与分叉级数无关) [10] ,即
、
、
。
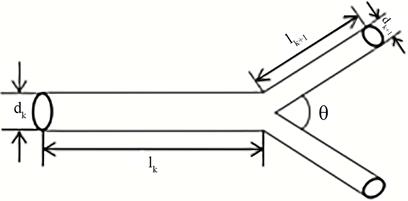
Figure 2. The kthsingle bifurcation of a fractal bifurcating network
图2. 分形分叉网络的第k级单分叉结构
许多研究表明,当两种不相混溶流体同时流过多孔介质时,它们往往会有不同的流动路径,气相流体会占据大孔隙,而液相流体会占据小孔径 [3] [12] 。为了区别气相和液相流体,假设存在一个临界半径
,母管半径小于该临界半径的所有分叉网络都被液体占据,而母管半径大于该临界半径的所有分叉网络都被气体占据 [13] 。考虑一个单元横截面,则液体的饱和度可以表示为:
(8)
由此可以得到临界半径
的表达式:
(9)
根据Hagen-Poiseuille方程,单根分形分叉网络中气液两相流的流量可以表示为:
(10a)
(10b)
对方程(10)进行积分,结合方程(9)得到裂缝网络气液两相总流量为:
(11a)
(11b)
在上述推导中,使用了
和
。运用广义达西定律:
(12)
其中特征长度L定义如下:
(13)
联立方程(5)和(11)~(13),得到裂缝分叉网络气液两相流的渗透率:
(14a)
(14b)
对于饱和多孔介质,每根分叉管道里只充满一种流体,因此,饱和裂缝网络的绝对渗透率可以表示为:
(15)
联立方程(14)和(15)可以得到裂缝网络的相对渗透率:
(16a)
(16b)
2.2. 双重介质渗流模型
将各向同性多孔材料作为基质,利用分形分叉网络嵌入到基质材料中形成双重介质模型,用以研究裂缝型多孔介质的气液两相渗流特性。通常分叉裂缝起主要的渗流作用,而大量的流体储存在低渗透的母体基质。Journel等人 [14] 提出有效渗透率
可以表示成局域渗透率的幂平均:
(17)
其中V是平均体积,幂指数
符合
,其值取决于材料的性质,一般可以由实验数据拟合得到。实际上,多孔介质中的渗流管流化越明显,低渗流区域越少,有效渗透率越接近算术平均值(
)。因此,为了简化计算,假定有效渗透率可以近似为网络和母体基质渗透率的算术平均值。对于双重多孔介质气液两相有效渗透率,方程(17)变为:
(18a)
(18b)
其中
、
分别表示基质多孔材料的气相、液相渗透率;
、
分别表示裂缝网络的气相、液相渗透率,其值可通过方程(14)计算得出;
和
是母体基质和分叉网络的体积分数(
)。
对于总分叉级数为m的单根分叉网络,网络体积为:
(19)
对母管半径在
范围内积分可得分叉网络的总体积
,与渗流区域的总体积V相比即可得到裂缝网络的体积分数:
(20)
相应地,母体基质材料的体积分数
。
3. 有限元模拟
由于裂缝在渗流等流体输运过程中通常扮演流体流动的首选和主要通道,对于流体渗流过程起主导作用,母体基质多孔材料的渗透率通常较小,故母体基质的渗透率远远小于裂缝网络的渗透率 [9] 。因此,本文使用COMSOL Multiphysics建立树状裂缝的气液两相流动模型。通过最小化流阻原理得到最优化结构参数 [10] ,即
和
,设置第0级管道的长度和半径分别为
和
。采用以下边界条件和初始条件:
(1) 选择甲烷作为气相,水作为液相。网络在初始条件下充满气态甲烷,左侧被液体置换,流体从右侧流出;
(2) 模型左侧为压力入口,边界符合狄利克雷边界条件的要求,压强为10 Pa,流体禁止回流,无切向速度;
(3) 模型右侧为出口,并设定出口压强为0 Pa,允许流体为气液混合,允许切向速度;
(4) 模型管壁为封闭边界,与外围无流体交换。
通过Navier-Stokes方程结合水平集方法构建气液两相渗流数学模型,其动量守恒方程如下:
(21)
(22)
其中
为流体密度,p为速度矢量,u为t时刻的速度分量,I为单位对角矩阵,
为粘度,F为单位体积流体受到的外力。
水平集方法是界面跟踪和形状建模中常用的一种数值模拟方法,其基本思想是将流体流动界面抽象为一个高维空间,通常用水平集函数的零水平集表示。通过界面水平集方程的不断迭代演化,直至稳定,得到流动界面的形状。在裂缝网络气液两相流模拟过程中,水平集函数可以描述气液两相界面形状的动态变化特征,其界面变化的方程可写成:
(23)
流体的性质控制方程如下:
(24)
(25)
其中,
为水平集变量,一般取值为
,
表示气相,
表示液相,通常将取值为0.5的等值面作为相界面;
为界面厚度控制参数;
是水平集函数初始化参数,一般为流体流动的最大速度;
和
分别为气液两相的密度;
和
分别为气液两相的粘度。
4. 结果与讨论
4.1. 结果验证
在验证的过程中,将最小最大孔径比设定为
,孔隙率为
。根据方程(4)可以得到分形维数
。数值计算结果表明液体从左侧入口进入分叉管道,沿着管道对气相进行驱替,其体积分数如表1所示。

Table 1. The volume fraction of fluid at different times in a fracture network
表1. 裂缝网络不同时刻下流体体积分数
根据简化后的达西方程计算渗透率:
(26)
其中
为出口流体的流速,
为达西速度。将数值模拟计算得到的气液两相相对渗透率与方程(16)的分形模型进行对比分析,如图3所示。进一步地,将分形模型预测的相对渗透率与实验数据(
,
) [15] [16] 对比,如图4所示。在很低的液体饱和度下,液相相对渗透率接近于零,而当饱和度达到1.0时,液相相对渗透率则接近于1.0;气相的相对渗透率则与液相相对渗透率相反。由图3和图4可以发现,分形模型的预测结果与有限元模拟和实验数据较为吻合,验证了分形模型的合理性和正确性。
图3. 分形模型预测值与有限元模拟对比图
图4. 分形模型预测结果与实验数据对比图:(a)
;(b)
4.2. 参数化分析
图5. 分形维数与孔隙率以及最大最小孔径比之间的关系
图6. 孔隙率和分形维数对相对渗透率的影响规律
根据方程(4)可知孔隙分形维数
、孔隙率
以及孔径比
之间存在内在关联,如图5所示,在固定的孔径比
,分形维数随孔隙率的增大而快速变大,当孔隙率趋向于1.0时,此时孔隙几乎填满整个平面,因此孔隙分形维数趋向于2.0;在相同孔隙率条件下,分形维数随孔径比的减小(孔隙范围变大)而增大,孔隙结构越复杂。如图6(a)所示,在特定的液体饱和度下,分形维数的增加意味着孔隙率的提高和孔隙尺度的增加,而气相占据较大尺寸孔隙,因此气相相对渗透率随着分形维数的增加而提高,而液相相对渗透率随着孔隙分形维数的增加而显著降低。而图6(b)显示,在相同孔隙率和液相饱和度条件下,分形维数对于气相相对渗透率的影响较小,而液相相对渗透率随着孔隙分形维数的增加而降低,但幅度也较小。由此可见,裂缝网络的结构对于气液两相渗流具有显著的影响。
5. 结论
本文基于分形几何理论建立了裂缝型多孔介质气液两相渗流模型,得到了气液两相相对渗透率的解析表达式,并利用有限元方法建立了裂缝型多孔介质的气液两相渗流的数学模型。结果表明,裂缝型多孔介质气液两相渗流的分形模型预测结果与有限元模拟以及实验数据吻合较好,相对渗透率主要依赖于裂缝结构特征和气液两相分布特征。气相相对渗透率和液相相对渗透率随着液相饱和度的增加而降低和提高,且在特定液体饱和度的情况下,增大裂缝孔隙分形维数可以提高气相相对渗透率和降低液相相对渗透率。相比较而言,孔隙率对于相对渗透率的影响更为显著,但在相同孔隙率条件下,孔隙微细结构的差别(分形维数不同)仍然对于气液渗流产生较为明显的影响。本文提出的分形双重介质模型为裂缝型多孔介质渗流机理研究以及页岩气高效开采等领域提供了一种有效的数学方法和理论依据。