1. 引言
在现代电力系统中,随着风能、太阳能等可再生能源的渗透,发电的主要来源并不总是稳定的,而是在不同的时间范围内急剧波动 [1]。对于大型风电场来说,这个问题更加明显,风速的显著变化会影响电网侧的发电量 [2]。此外,由于风机故障无法运行或风机维护等意外事件,一个或多个供给装置可能无法运行。因此,风电场的发电量和电流特性在一年中不同的月份或季节可能会有较大的差异。
论文 [3] 中表明,在故障状态和正常运行状态,上述情况会给电力系统保护继电器、协调及其性能带来严重的问题。例如,如果风电场的一个风力涡轮机正在进行维护,该风力涡轮机将处于离线状态,不会向电网输送任何电力,在风力涡轮机故障时与所有风力涡轮机都在运行向电网提供电力 [4] 时的风电场产生的电流特性完全不同。因此,如果继电器是静态的,不根据风电场的动态行为调整其设置,将导致保护继电器 [5] 的不协调、不灵敏、盲目和误操作。在这种情况下,可能严重损坏电力设备,降低电能质量、稳定性、安全性和风力发电场的可靠性。因此,针对上述问题,设计适合风力发电场的保护方案迫在眉睫。
论文 [6] 中提出了一种风电场长距离输电线路的自适应距离保护方案,通过集成的方法改变继电器特性,可以自适应地改变距离保护的设置,并同时考虑到了晶闸管控制的串联补偿、风电和故障电阻的不利影响因素。在论文 [7] 中,针对连接海上风电场的高压直流电压源变换器,提出了一种基于自适应下垂的分级最优电压控制方案。通过协调风力涡轮机和风电场电网侧VSC,最小化风电场内部总线的电压偏离标称电压,从而缓解无功功率(VAR)波动。一些研究人员还考虑设计一种自适应重合闸风电场高渗透电网方案 [8] [9]、考虑局部风电场谐波对故障发生时继电器性能的影响。
为此,本文提出了一种新的基于灰狼优化算法(GWO)的自适应大型风电场过流保护方案,可显著提高风电场运行的安全性和可靠性。本文建立了一个大型风电场的模型,用于进行故障分析、继电器设置和协调计算。采用GWO实现了过电流继电器(OCR)的最佳协调,并通过仿真和实验结果验证了提出的GWO技术用于提高风电场保护的可靠性和高效性,并与其他流行的高效优化技术进行了比较,其中,所提出的GWO自适应最优保护协调方案具有较好的性能。
本文的组织结构如下。第二节介绍了灰狼优化算法(GWO),第三节介绍了最佳OCR协调的GWO技术,第四节给出了仿真和实验结果,并进行了适当的讨论和分析。最后,第五部分对本文进行了总结。
2. 灰狼算法
灰狼优化算法(GWO),通过以下优点局部最优避免、达到全局最优值、无求导机制、灵活性和简单性,得出最佳解决方案 [10]。GWO算法是基于种群的优化算法,它模拟了自然界灰狼的领导层级和狩猎机制。灰狼具有非常严格的社会等级层次制度,见图1,图中第一层是种群中的领导者,称为α,是算法中的最优解。
图中第二层是领导者α的智囊团,称为β,是算法中的第二最优解。图中第三层是在种群中负责侦查做事的工人,称为δ,是算法中的第三最优解。在算法中,适应度不好的α和β也会降为δ。图中最底层是ω,是算法中的备选解。
GWO算法流程图见图2。

Figure 2. General flowchart for grey wolf optimizer algorithm
图2. GWO算法通用流程图
在狩猎过程中,灰狼有包围猎物的倾向;因此,可以为此类行为设计如下数学模型:
(1)
(2)
上述方程中,D表示个体与猎物间的距离,为正值,A和C是系数向量,t为迭代代数,Xp和X分别是猎物和灰狼位置向量。
A和C系数向量的计算如下:
(3)
(4)
在迭代过程中,其中,“a”是收敛因子的值从2线性减少到0,而r1和r2是[0, 1]中的随机向量。在迭代过程中,选择最多的三个最优解,根据其以前的最佳位置更新其位置。这个阶段的公式为:
(5)
其中,Dα,Dβ和Dδ分别表示α,β和δ与其他个体间的距离;Xα,Xβ和Xδ分别代表α,β和δ当前位置;C1,C2和C3是随机向量,X是当前灰狼个体的位置。
(6)
(7)
X1,X2和X3分别表示狼群中ω朝向α,β和δ前进的步长和方向,A1,A2和A3是随机向量,X(t+1)是ω的最终位置。
3. 基于GWO算法优化
为了优化OCR协调,设定一个特定的目标函数(OF)。由于这项工作的目标是最小化继电器的总运行时间,初步OF可以写为:
(8)
上式中,ti是OCR的运行时间,X1是权重因子。OF函数是求OCR的操作时间最小值;但是,未考虑到协调时间间隔、时间倍增器设置(TMS),这些协调约束也应添加进去,确保继电器之间出现不协调。因此,提出系数
,式中,Δtmb是继电器的间隔时间。约束条件如下:
(9)
最终OF公式如下:
(10)
OF中的第一项是OCR操作时间的总和,第二项是协调约束,以及X1、X2和Y是加权因子。ti表示OCR的工作时间,由IEC 60255-151:2009标准(17)推导而来,相应替换为公式(10),首先计算每个继电器的TMS,然后得到TMS的最优值。Δtmb是区别主保护继电器和备用保护继电器之间的时间。
权重因子X1、X2和Y需要定制取决于优化应用程序。在基于GWO的仿真过程中通过试错法测试最优的权重因子,选定的最优参数为:X1= 1、X2= 2和Y = 100,以便OF达到每个OCR的最小TMS值。
4. 仿真
假设风电场由40台风力涡轮机组成,每台风力涡轮机产生1.25 MVA功率,在575 V电压水平和60 Hz频率下运行。风机升压变压器额定功率为1.5 MVA,将风机电压从575 V提升至35 kV,Y侧接地的Y-Δ连接。整个风电场通过升压变压器和输电线向主公用电网累计馈电50 MVA。线间电力变压器额定功率为60 MVA,在Δ-Y连接中将风电场电压从35 kV提升至220 kV,其中Y侧接地。线间输电线路长度为50 km,建模为三相四线,由R-L串联阻抗和两组并联电容组成,集中在线路的起点和终点,如图3所示。
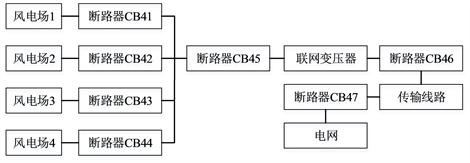
Figure 3. Simplified model of the designed large-scale wind farm
图3. 大型风电场简单模型设计
每个风力涡轮机和风力涡轮机旁边的电力变压器都由高压侧的OCR保护,相应断路器标志为CB1、CB2、……CB40。每个风电场本身都由另一个OCR和CB保护,见图3中所示的CB41-44。靠近线路侧的电力变压器低压侧的整个风电场集电器部分由CB45保护,而变压器高压侧由CB46保护。最后,连接整个风电场和电网的输电线路由CB47保护。
GA优化技术是最稳健和高效的优化算法之一。为了进行比较,选择GA算法作为对比算法,图4显示了每个继电器在TMS方面的最佳解决方案。
接下来,为每个组设置实施基于GWO的优化技术,以优化TMS和OCR的操作时间。优化过程中,个人之间的平均距离越小,结果越好。在模拟开始时,适应度函数(OF)最优的个体值非常大,这意味着结果不是最优的。在GWO优化过程中,适应度函数开始显著减小,并达到平均距离的临界点。此时,结果变得稳定,无法进一步改善(收敛到最小值)。即认为,GWO已成功获得最佳值,得到每个继电器组设置的TMS (即运行时间)最小值。收敛后,每个继电器的最佳TMS设置如图5所示,与GA相比,GWO算法给出的TMS更小,其结果明显更好。
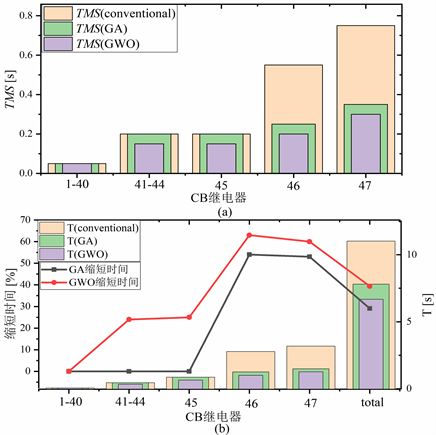
Figure 6. Comparison of coordination methods of GWO, GA and conventional relays
图6. GWO、GA和常规继电器协调方法比较
图6所示为GWO、GA和常规继电器协调方法比较。其中图6(a)为三种算法给出的各台继电器的TMS值,图6(b)为三种算法给出的总时间T与GWO、GA相对常规方法的时间缩短百分比。由图可知,相对常规继电器协调方法,GA算法能降低继电器的TMS和总时间T,而所提方法对T的减少量相对GA算法更为显著,最多能比GA算法多减少25% (45号继电器),证明了所提方法在大型风电场的继电器协调优化中优于其他技术。
5. 结论
本文提出了一种基于GWO的大型风电场自适应最优过流保护方案。虑到协调时间间隔、时间倍增器设置(TMS)等协调约束,提出了一个OF,以通过GWO优化最小化OCR的TMS值(即继电器的运行时间)。通过仿真将所提GWO的性能与常规继电器协调方法和GA优化的性能进行了仿真对比。结果表明,所提方法能得到更低的OCR的TMS值,改善电场的OCR运行时间,具有更优异的性能。