1. 引言
随着社会不断发展和人民生活水平的提高,对电力的需求逐渐增大,提高电力传输效率对电力系统运行极为重要。在一定边界约束下通过控制无功功率的供需平衡与分布特性,可以降低电力系统的网损 [1]。随着绿色理念的引入,目前电力系统中新能源并网比例也逐渐增高。截至2020年,我国已成为首个风电装机容量达200 GW的国家,紧随而来的是电网网损激增,传输效率下降。因此需控制多种无功调控资源来协调优化,解决或缓解网损激增问题。
针对无功优化来降低网损相关问题的研究成果较多。根据配电网在无功优化算法方面,文献 [2] 采用基于差分进化的粒子群算法进行多目标无功优化,提高了粒子群算法的性能。文献 [3] 结合粒子群算法和禁忌搜索TS算法两者的优点针对有功网损,电压稳定裕度和电压偏差三个方面分成两个时间段进行运算实现无功优化。在新能源并网后的优化控制方面,文献 [4] 针对风力发电及火力发电的优缺点和经济性能进行了一定的比较,分析两者在能源发电上的发展前景。文献 [5] 针对新能源并网会导致风电渗透率,并对其产生的一系列问题进行调控分析,采用新英格兰10机39节点对研究内容进行验证。文献 [6] 采用免疫与遗传算法结合,解决分布式新能源并网导致电网不稳定的问题进行无功优化分析。根据优化的目标函数采取,文献 [7] 构建了多目标无功优化模型。文献 [8] 采用Matpower对IEEE30节点系统的无功优化研究,文献 [9] 基于PSO采用粒子群算法,通过非线性权重设计目标函数对10机39系统进行风电并网的分析与无功优化。本文在前人研究的基础上,针对含风电系统无功调节能力有限的特点,将多种无功调控资源纳入调节范围,研究无功优化方法,符合新能源发展的需要和节能环保的主题。
含大规模风电系统中,除了常规火力发电机外,并网风电机组一般配置有静止无功补偿器(SVC)。因此本文将常规机组,风电机组,SCV,电容电抗及变压器分接头均作为无功调控资源,进行协调控制。以全网网损最小为优化目标,在一定的条件约束下建立优化模型,并采用粒子群算法进行求解。基于改进的IEEE30节点标准电网模型,来实现无功优化,寻找高比例新能源电力系统无功最优调控方法及控制策略。
2. 多无功调控资源的优化控制模型
2.1. 多无功调控资源能力分析

Table 1. Comparison of multi-reactive power control resource performance
表1. 多无功调控资源性能比较
多无功调控资源性能比较如表1。
为满足无功调控需要,采用多无功源协调配合。其中电容发出无功,电感吸收无功,可以进行就地无功补偿,从而减少有功损耗;SVC通过晶闸管控制电抗器和电容器可以连续调节补偿装置的无功功率,且调节速度极快;常规发电机组也可发出无功,适用于发电厂附近节点的调配,需要时也可吸收部分无功;对于风力发电机组,无功调节能力有限;变压器分接头适合改变无功分布。
2.2. 多无功源优化控制模型
2.2.1. 目标函数
本文仅考虑单个目标,即有功网损最小,如式(1)所示:
(1)
式(1)中
为网损,
为常规发电机组有功功率,
为常规发电机组组数;
为风力发电机组有功功率,
为风力发电机组组数;
为负荷功率,
为负荷组数。
2.2.2. 约束条件
等式约束条件:
等式约束条件一般为各母线潮流方程,即有功功率和无功功率保持平衡,在极坐标系下:
(2)
(3)
式(4) (5)中,
,
为节点号;
为当前系统拥有的总节点数;
、
为支路电导;
为节点电压相角。
,
为电路中电导和电纳。
不等式约束条件:
不等式约束条件一般为一些安全限制:
(4)
常规发电机组有功功率
,无功功率
,风力发电机组有功功率
,无功功率
,节点电压大小
、变压器分接头的调节范围
、电容器容量
和SVC无功出力上下限
不得逾越的限额。
对于功角:
3. 基于粒子群算法的多无功调控资源优化控制方法
3.1. 粒子群算法基本原理
粒子群算法(PSO) [10] [11] 是由美国学者Kennedy和Eberhart在1995年提出的一种进化计算算法,这种算法的基本思想来源于对鸟群捕食行为的观察和模拟带来的启发,核心思想是将实际问题的解具象为多个具有记忆属性的粒子,通过设定粒子的存在空间范围、移动速度、移动方向等一系列限制条件,让粒子不断更新自身位置,多次迭代寻找趋于最优的解。
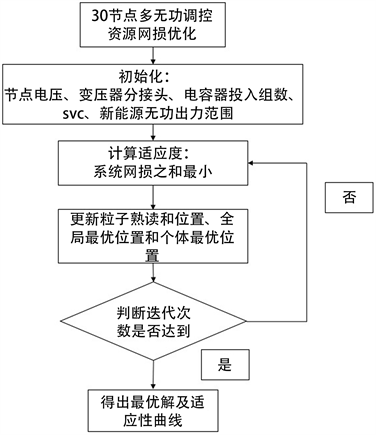
Figure 1. Optimization control flowchart of multi-reactive power control resource based on particle swarm algorithm
图1. 基于粒子群算法的多无功调控资源优化控制流程图
其中:
为粒子
的第
维在第
次迭代时的速度;
为粒子
的第
维在第
次迭代时的位置;
为惯性权重,
、
为加速学习因子,
、
为[0, 1]间的随机数,
为粒子当前的个体最优位置,
为粒子当前的种群最优位置。具体迭代算法流程如图1所示。
3.2. 多无功调控资源优化控制方法
本文基于粒子群算法,对含有新能源发电机组的电网进行多无功源的无功电压优化。首先将粒子 多维化,在第一维设置传发电机,第二维设置变压器分接头,第三维设置电容组,第四维设置svc设备,第五维设置新能源无功出力,这样就实现了新能源发电机接入电网,再将多维的粒子进行粒子群算法的迭代运算,根据设置的适应性方程判别,寻找最优解,最终实现对含有新能源发电机组的电网的多无功源无功优化。
4. 算例分析
4.1. 算例设置
本文基于粒子群算法,对含有新能源发电机组的IEEE30节点系统(如图2)进行无功优化。该系统中包括3个风力发电场(位于节点1、22、13),三个火电厂(位于节点2、27、23),四台变压器(位于6-9、6-10、4-12、28-27),两个电容器组(位于节点10、24),三台静止无功补偿装置SVC (位于节点1、22、13)。
变压器分接头设置8个档位,分别为
p.u.,电容器组投入无功容量(单位:Mvar)分别为
,投入SVC的无功范围(单位:Mvar)为[−30, 30]。
风电场(节点1, 22, 13)与火电厂(节点2, 27, 23)的参数如表2所示:
4.2. 算例结果分析
算例运算结果如表3所示:
本算例中,静止无功补偿装置SVC与新能源位于相同节点,因此,相应的节点无功上下限应为二者无功上下限之和,发电厂节点优化结果见表4。

Table 2. Power plant node parameters
表2. 发电厂节点参数

Table 4. Power plant node optimization results (Mvar)
表4. 发电厂节点优化结果(Mvar)
其余节点电压标幺值优化结果见表5:

Table 5. Optimization results of ordinary nodes (nominal values)
表5. 普通节点优化结果(标幺值)
由表5可知,优化后节点电压均未越限,因此,该算法可用于对含新能源的电力系统进行无功电压优化。并且成功降低了有功网损(单位:MW),有功网损有名值优化结果如表6:

Table 6. Active network loss optimization results (MW)
表6. 有功网损优化结果(MW)
经过粒子群算法优化,使得带有风电场的IEEE30节点系统的有功网损降低21.53%。
适应度曲线如图3:
由适应度曲线得知,粒子群算法优化IEEE30节点系统有功网损时,适应度在第32代时不再降低。
5. 总结
本文根据现有时代背景提出改进新能源发电的无功优化控制方法的策略研究,能够对系统的无功容量在受限范围内进行控制,对含风电场的有功网损进行优化,并采用了粒子群算法求解该优化问题,可以快速得到优化方案,计算成本低。仿真结果表明:通过本文所述基于粒子群的优化方法,能够优化多种无功调控资源,有效减小含风电场系统的有功网损。可进一步研究改进算法来提高跳出局部最优的能力。
基金项目
中央高校基本科研业务费专项资金;中国矿业大学(北京)大学生创新训练项目(202104032)。