1. 引言
近年来,随着人民生活水平的提高和产业结构的调整,我国电网峰谷差逐年增大,电网调峰任务日渐突出 [1]。另外环境污染严重,己引起社会的广泛关注。中科院研究表明:北京空气PM2.5污染颗粒中18%是由燃煤造成的,这与中国北方冬季采暖燃煤为主不无关系 [2]。将用电低谷时期的大量富余电能以热能的方式储存并用于供暖,可以平衡用电负荷的变化,提高电网效率和安全性,减少环境污染,是一种统筹社会效益和经济效益的有效途径。从目前的应用情况来看,显热储热因其价格较低且装置结构简单,应用范围较广。固体混凝土储热相对具有良好的应用前景。Laning D等 [3] [4] [5] 对混凝土蓄热技术进行了大量的试验,开发测试了高温混凝土蓄热示范模块。其中,该团队以混凝土为蓄热介质,建立了固体蓄热模块,测试了500℃以下材料的稳定性以及200℃~500℃环境中长期蓄热时材料的损耗,通过循环实验与仿真认为混凝土是适合高温蓄热的材料。武汉理工大学朱教群等 [6] [7] 开发了耐高温混凝土,并对混凝土储热系统的强化换热以及提高混凝土导热系数的方法进行了研究。但是固体混凝土蓄热目前仍存在很多问题,限制了其的应用和推广。
固体混凝土储热材料相对相变储热材料来说储热密度低,这意味着想要储存更多的热量,需要增加工作温度或者增大装置体积。增加工作温度,使蓄热装置处于高温状态,一方面需要较大的加热管功率,这对加热管的寿命和用电安全产生更高的要求。另一方面装置的高温环境对各个部件耐高温的性能要求较高,这类零部件的价格一般高于普通产品的一倍,导致装置的基础成本偏高;同时也增加了保温的难度,导致整个装置漏热严重,电能转化为热能输出到用热端的整机效率较低,与能源高效利用的理念背道而驰。增大装置体积,则使整个装置占地面积增大,耗用成本增加,不适用于供热的需求。
熔盐蓄热材料,具有“四高三低”的优势,是近年来国内外研究的热点 [8]。熔盐作为典型的潜热蓄热材料,储能密度高、温度变化范围小,利用此优势,可达到减小蓄热系统的体积,节约成本。彭达文等 [9] 为了得到混合熔盐在单罐蓄热系统内的相变传热规律,针对具有低熔点的四元混合硝酸盐展开研究,采用VOF与焓–多孔介质耦合模型对底部加热条件下蓄热单元内相变材料的相变蓄热过程进行模拟,并利用实验进行验证。结果表明:相变过程中罐内出现明显的温度分层现象,固液界面出现波动。蓄热单元中所产生的自然对流强弱直接影响热量传递,同时固液相界面的位置决定自然对流的发展。Cabeza L F等 [10] 研究了加装相变蓄热模块对显热蓄热为主的蓄热水箱的性能的影响。将乙酸钠(熔点为58℃)封装在圆柱管中作为相变蓄热单元,结果显示将2个单元放置在蓄热水体的上部可以提高约40%的蓄热量,相变蓄热和显热蓄热的结合是有效的。
本文针对混凝土和混凝土–熔盐两种蓄热结构,通过数值模拟进行相应的分析,技术流程图如图1所示。在混凝土蓄热装置中加入封装的熔盐相变层,目的在于增加混凝土蓄热装置的蓄热量,提高整个装置的经济性,为电蓄热供暖系统的应用提供技术参考。
2. 物理模型
低谷电通过电加热器加热蓄热介质,蓄热介质温度升高,电能变为热能进行储存。本文蓄热装置的单元模型为圆柱形结构,圆柱形外壁面布置等高的电加热器,圆柱形内部填充混凝土作为蓄热材料,在混凝土的中间加入采用不锈钢封装的环形熔盐相变层,整个蓄热装置为对称的结构,简化为如图2所示的二维结构。模拟计算采用如下基本的假设:
1) 混凝土各向同性,物性参数为常数,不随温度发生变化;
2) 熔盐各向同性,固液状态中除密度外其他物性参数为常数,不随温度发生变化;
3) 不考虑封装熔盐的不锈钢材料的厚度;
4) 不考虑熔盐相变过程中的体积变化;
5) 蓄热体上下表面为绝热边界。
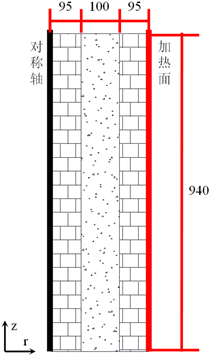
Figure 2. Schematic diagram of concrete-molten salt heat storage structure
图2. 混凝土–熔盐蓄热结构示意图(单位:mm)
计算区域中,混凝土采用武汉理工大学朱教群团队 [7] 研制的耐500℃的高温混凝土,熔盐采用文献 [11] 自主研发出的四元混合硝酸盐,其相变起始温度为96.8℃,最高使用温度600℃。两者的物性参数如表1所示。

Table 1. Physical properties of concrete and molten salt
表1. 混凝土和熔盐的物性参数
其中当不考虑熔盐的自然对流时,熔盐密度取平均密度
3. 数学模型
本文使用热焓模型,将相变区域看成多孔介质,根据空隙率来判断材料所处的相态。
3.1. 控制方程
在上述假设的基础上,整个计算区域内的流体流动及传热满足以下微分方程组 [12]:
连续性方程:
(1)
式中:u为流体流速;t为时间;
为流体密度。
动量方程:
r方向:
(2)
式中:p为流体压力;
为流体运动粘度;
为糊状区孔隙率函数。
z方向:
(3)
(4)
其中,g为重力加速度;参数
是一个接近0.001的常数,避免分母为0;常数C为相当大的数,本文中取104。
能量方程:
(5)
式中:T为温度,
为导热系数。
能量方程中h为比焓:
(6)
其中,
为参考温度下的比焓;L为潜热;
为定压比热容。
液相分数定义为:
(7)
其中,
为相变蓄热材料凝固温度;
为相变蓄热材料熔化温度。
3.2. 边界条件
加热面采用等温加热
;
上下表面为绝热边界条件:
;
熔盐和混凝土的初始温度为300 K;
熔盐和混凝土的接触面为耦合壁面:
,
。
4. 数值求解
4.1. 网格无关性验证
用CFD前处理软件Mesh对模型进行网格划分,划分情况如图3所示。在加热面附近,由于温度梯度大,采用局部网格加密。分别取网格数为3583、5424、12,596、33,318、72,428、126,911进行模拟,模拟1小时后,统计相变层的液相率如图4所示。从图4可以看出,当网格数达到72,428时,液相率达到平稳,综合考虑计算时间和准确度,采用网格数为72,428。
4.2. 求解器的设置
本文采用的数值方法是基于原始变量的SIMPLE方法,压力项采用PRESTO!方案离散,动量方程和能量方程采用二阶迎风格式进行离散,采用的时间步长为0.5 s。
5. 数值模拟结果与分析
5.1. 自然对流对蓄热过程的影响
当熔盐的密度为常数时,相变层内的传热方式只有导热,此时即忽略熔盐区的自然对流。当熔盐的密度是随温度变化的函数时,发生相变以后,温度高的熔盐区域密度小,温度低的区域熔盐密度大,温度的不同导致熔盐密度的不同,密度差诱发自然对流的发生。此时熔盐发生相变后不仅存在导热同时也存在自然对流。为了探究自然对流对熔盐融化过程的影响,模拟加热8小时后的熔盐液相率云图如图5和图6所示。
由图5可以看出考虑自然对流时,刚开始熔盐平行于加热面融化,但是随着固液相熔盐的密度不同,融化后的熔盐开始流向相变层的上方,熔盐从上往下开始融化。图6中忽略自然对流时,熔盐区域不存在密度变化引起的流动,固液分界面平行于加热面,熔盐依次融化。由图7可以看出考虑自然对流时熔盐从0.5 h小时开始融化,在3.5 h全部融化完毕,全部融化时间为3 h。忽略自然对流时,开始时熔盐的融化速率明显要慢于考虑自然对流时的速率。从0.5 h开始融化,8 h全部融化完毕,融化时间为7.5 h,融化时间比考虑自然对流时增长了114%。对于相变蓄热来说,只有快速融化,才能发挥潜热的优势,同时产生自然对流,对蓄热起到促进作用。因此对于相变材料来说,融化过程中考虑自然对流是有效的,也是有必要的。
为了比较自然对流对复合体蓄热量的影响,每半个小时对蓄热体的蓄热量进行统计,数据结果如图8所示。从图8可以看出在熔盐未融化时,两者的蓄热量相当,而随着熔盐的融化,两者开始产生差异。在熔盐融化的前期两者进行相比,考虑自然对流情况的蓄热量略低,显示出了熔盐导热系数低所导致的热阻效应。但是随着融化的进行,熔盐潜热的作用和融化区自然对流的增强,考虑自然对流的蓄热量开始反超,并在8 h后,达到了35731.8 KJ,相比于忽略自然对流33462.9 KJ的蓄热量,增长了2268.9 KJ,增长率为6.8%。综上所述,从融化速率和蓄热量的情况来讲,对于以上复合蓄热结构必须考虑熔盐自然对流的影响。固下文所讨论的复合体即为考虑了熔盐自然对流的复合蓄热体。

Figure 4. Grid independence verification diagram
图4. 网格无关性验证示意图
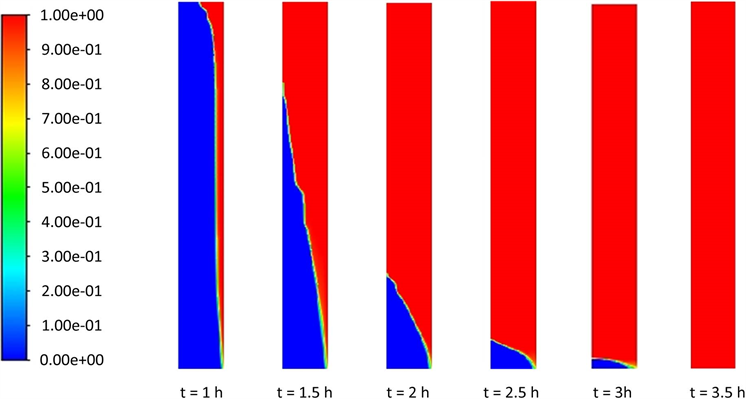
Figure 5. Liquid phase cloud diagrams considering natural convection
图5. 考虑自然对流的液相率云图

Figure 6. Liquid phase cloud diagrams ignoring natural convection
图6. 忽略自然对流的液相率云图

Figure 7. Relation curve of liquid phase ratio of molten salt with time
图7. 熔盐的液相率随时间变化的关系曲线
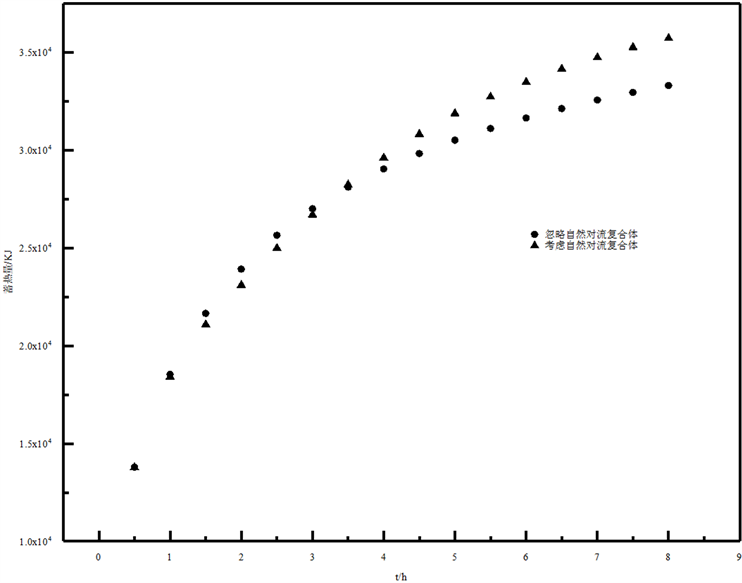
Figure 8. Schematic diagram of heat storage over time
图8. 蓄热量随时间变化的示意图
5.2. 蓄热过程温度分布的比较
加热面的边界条件为恒温加热,蓄热体内的温度分布对蓄热量有一定的影响,只有靠近加热面的温度较低,产生较大的温差才能保证蓄热量的增大。为了比较复合体和混凝土蓄热过程的温度分布,得到温度分布的数值模拟结果如图9所示。从图9可以看出,复合体内的温度分布不均匀,相变层内的自然对流,导致高温熔盐集中在熔盐的上部,整个蓄热体的上方温度明显比下方温度要高。自然对流的作用导致热量向对称轴侧的混凝土区快速传递,从温度云图可以看出,复合体对称轴侧的混凝土的平均温度要高于纯混凝土蓄热体,这个区域的显热蓄热能力被进一步利用。纯混凝土蓄热体呈现明显的温度分层,并且温度分布平行于加热面。
5.3. 蓄热量的比较
对于混凝土蓄热结构来说,加热过程中蓄热量是以显热方式进行储存的,而在混凝土–熔盐蓄热结构中由于涉及到熔盐的相变过程,熔盐区域的蓄热过程是显热–潜热–显热的方式。熔盐融化后的自然对流对蓄热过程的影响,导致复合蓄热体的蓄热过程要复杂一些。为了清晰的比较和分析加入熔盐相变层后对复合体结构的蓄热过程和蓄热量的影响,对两种结构进行分区比较。混凝土结构按照复合体的结构进行相应的分区,复合体分区示意图如图10所示。

Figure 9. Temperature map of the thermal storage body over time (left: composite, right: concrete)
图9. 蓄热体随时间变化的温度云图(左:复合体,右:混凝土)
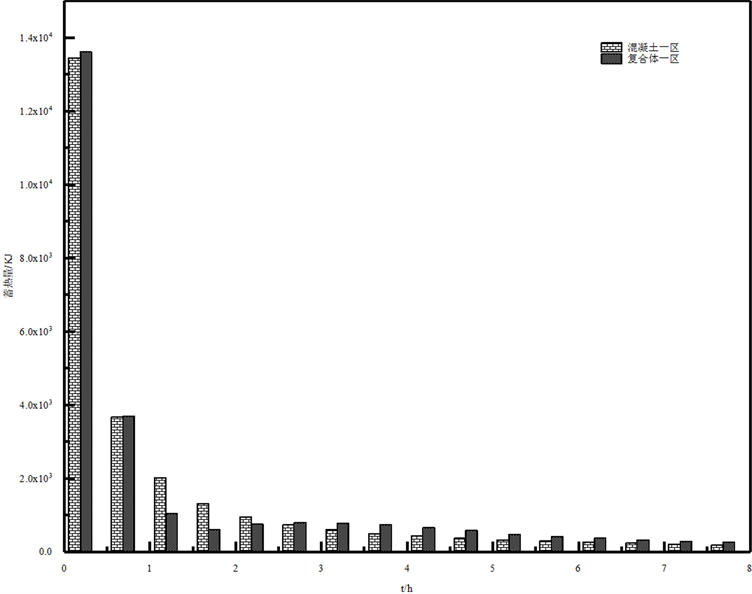
Figure 11. Schematic diagram of the heatstorage capacity of the first zone over time
图11. 一区的蓄热量随时间变化的示意图
相变层的加入对复合体蓄热量的影响,不仅仅体现在熔盐的相变潜热,增加了二区的蓄热量,同时由于自然对流的产生也会对一区和三区混凝土的蓄热量产生影响。从图11可以看出,复合体一区蓄热量呈现快速减小的趋势,减小一方面是因为混凝土中温度升高导致和加热面的温差减小,蓄热量出现大幅度的减少;另一方面随着熔盐的融化,自然对流的作用导致一区蓄热量快速向熔盐区传热,也会出现蓄热量的减小。混凝土蓄热体一区蓄热量的变化趋势与复合体相似,但减小的速率较慢,这是因为减小的原因只是蓄热体内温度增加与加热面的温差变小。8小时后复合体一区蓄热量为25454.30 KJ,相比混凝土一区蓄热量为25595.27 KJ,减小140.97 KJ,减小率为0.56%。随着蓄热时间的进行,自然对流的产生,会使复合体一区蓄热量向熔盐侧快速传递,减小一区混凝土平均温度,使复合体能够储存更多的热量。
混凝土蓄热体中加入相变层以后,二区的蓄热形式发生了改变,从原来混凝土的显热蓄热变成了熔盐的显热和潜热蓄热。由于相变过程中潜热的作用,复合体的蓄热量一定会发生变化。为了分析熔盐层的加入,对二区蓄热量的影响,现统计两种蓄热结构二区的蓄热量如图12所示。从图12可以看出两种结构二区的蓄热量都是呈现先增加后减小的趋势,并能够明显的看出在熔盐相变的时间段内,复合体二区的蓄热量要明显多于混凝土二区的蓄热量,这主要是在相变的过程中,熔盐潜热造成的。蓄热刚开始时,热量没有大幅度传到二区,因此此时二区蓄热量比较少,随着蓄热过程的进行,二区蓄热量不断上升,会达到一个峰值,然后出现下降。这是因为蓄热过程中一区平均温度的不断上升,导致温差变小,对于恒温加热壁面来说,温差的减小,导致加入的热量减小,二区蓄热量随后也出现相同的响应。在加热后期的时间段内复合体二区蓄热量低于混凝土二区蓄热量,这是后期熔盐的自然对流作用使二区蓄热量向三区混凝土传递造成的。8小时后,混凝土二区蓄热量为85795.01 KJ,复合体二区蓄热量为94248.26 KJ,增长了8453.25 KJ,增长率为9.8%,这其中熔盐的潜热起了决定性的作用。

Figure 12. Schematic diagram of the heat storage capacity of the second zone over time
图12. 二区的蓄热量随时间变化的示意图
蓄热结构蓄热量的多少与蓄热体中蓄热物质蓄热潜力的充分利用有很大的关系。对于加热面为恒壁温的情况,靠近加热面的温度较高,而远离加热面的温度较低,这就会导致远离加热面处蓄热物质的蓄热潜力不能被充分利用,影响蓄热体整体的蓄热量。为了分析相变层的加入对蓄热潜力利用的影响,统计了蓄热过程中两种蓄热结构三区的蓄热量如图13所示。从图13可以看出两种结构三区蓄热量与二区蓄热量相似都是呈现先增加后减小的趋势。后期复合体三区蓄热量低于混凝土三区蓄热量,是后期此结构中,三区蓄热体的平均温度较大,温差较小的缘故。8小时后,复合体三区蓄热量为852.61 KJ,相比于混凝土三区蓄热量731.93 KJ,增长了16.5%。复合体中三区混凝土蓄热物质的蓄热潜力得到了更好的利用,这对蓄热体是有益的。相变层的加入对于改善蓄热过程,增加蓄热量是有效的。
相变层的加入对蓄热体各区的蓄热量都产生了一定的影响,为了更加直观体现整体蓄热量的变化,计算出了两种蓄热结构在不同时间整体蓄热量如图14所示。从图14可以看出开始阶段的复合体蓄热量是小于混凝土蓄热体的蓄热量,在相变层刚开始融化时,熔盐自然对流作用较弱,导热系数只有混凝土导热系数的五分之一,相变层结构对整个蓄热结构的传热有一定的阻碍作用。随着相变层的完全融化,熔盐潜热的热量吸收,复合体蓄热量出现反超,并在8小时后达到35731.74 KJ,相比于混凝土蓄热结构蓄热量的34906.71 KJ,增长了825.03 KJ,增长率为2.36%。相变层的加入对蓄热量的增加虽然有一定的促进作用,但是促进作用是逐渐显现出来的,并且在开始阶段还有一定的阻碍作用,此种结构适合比较长加热时间的蓄热过程中,在加热时间较短的蓄热过程中,相变层的优势不能充分显现出来。

Figure 13. Schematic diagram of the heat storage capacity of the third zone over time
图13. 三区的蓄热量随时间变化的示意图
5.4. 相变层相对加热面的距离对复合体蓄热量的影响
相变层相对加热面距离的结构图如图15所示,为了确定相变层在复合蓄热体结构中的位置,通过模拟计算了当相变层为100 mm,距离加热面55、75、95、115、135 mm时,8小时后复合蓄热体相应的蓄热量。比较相变层的相对位置对蓄热量的影响,得到了相变层相对位置与蓄热量规律的关系如图16所示。从图16可以看出,相变层距离加热面越远,复合体的蓄热量越多。对于混凝土结构8小时的蓄热量34906.71 KJ来说,当相变层距离加热面为55 mm时,复合体的蓄热量为30743.23 KJ,与之相比减少了4163.48 KJ。而当相变层距离加热面为135 mm时,复合体的蓄热量却达到了46183.57 KJ,与之相比增加了11276.86 KJ,增长率达到了32.31%。对于此复合体的结构来说,合理选择相变层的位置是极其重要的。

Figure 14. Schematic diagram of overall heat storage over time
图14. 整体蓄热量随时间变化的示意图
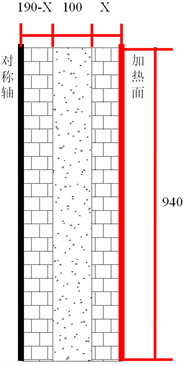
Figure 15. Structure diagram of phase change layer relative to heating surface distance
图15. 相变层相对于加热面距离的结构图(单位:mm)

Figure 16. Variation of stored heat with distance of phase change layer relative to heating surface
图16. 蓄热量随相变层相对加热面距离的变化图
6. 结论
本文是为了研究混凝土蓄热结构中加入相变层后对蓄热体蓄热过程和蓄热量的影响,并找出相变层合适的相对位置。通过对纯混凝土和复合体的数值模拟和分析之后,得出以下结论:
1) 相变层考虑自然对流是必要的,相对于忽略自然对流来说,考虑自然对流融化时间缩短56.25%,8小时后的蓄热量增加6.8%。
2) 复合体中因为熔盐相变层自然对流的影响,蓄热体内温度分布呈现上部温度高,下部温度低的不均匀性,而混凝土蓄热体内部呈现明显的平行于加热面的温度分布。
3) 相变层中熔盐的潜热作用和熔盐的自然对流促使混凝土蓄热能力被充分利用,导致复合体8小时后的蓄热量相比混凝土蓄热体的蓄热量增加2.36%。
4) 相变层的相对位置对蓄热量有一定的影响:当相变层距加热面135 mm时,复合体8小时后的蓄热量相比混凝土蓄热体的蓄热量增加32.31%。
基金项目
国家重点研发计划(2017YFB0903603)。